Question

如图，在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．

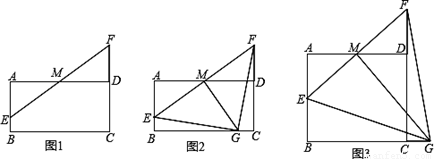
（1）如图1，求证：AE=DF；

（2）如图2，若AB=2，过点M作 MG⊥EF交线段BC于点G，求证：△GEF是等腰直角三角形

（3）如图3，若AB=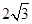，过点M作 MG⊥EF交线段BC的延长线于点G．

①直接写出线段AE长度的取值范围；

②判断△GEF的形状，并说明理由．

 

Answer 1

【答案】

（1）由△AEM≌△DFM可证得（2）关键是证GE=GF，再证有个角是直角。

（3）①＜AE≤． ②△GEF是等边三角形

【解析】

试题分析：解：（1）证明：如图1,在矩形ABCD中，∠EAM=∠FDM=90°，∠AME=∠FMD．

∵M是AD的中点，∴AM=DM，

∴△AEM≌△DFM（ASA）．

∴AE=DF．           2分

（2）证明：如图2，过点G作GH⊥AD于H，

∴∠A=∠B=∠AHG=90°，

∴四边ABGH为矩形，

∴∠AME+∠AEM=90°，

∵MG⊥EF，

∴∠GME=90°．

∴∠AME+∠GMH=90°

∴∠AEM=∠GMH．

∵AD=4，M是AD的中点

∴AM=2

∵四边ABGH为矩形，

∴AB=HG=2

∴AM=HG

∴△AEM≌△HMG（AAS）．

∴ME=MG．

∴∠EGM=45°．

由（1）得△AEM≌△DFM，

∴ME=MF．

∵MG⊥EF，

∴GE=GF．

∴∠EGF=2∠EGM=90°．

∴△GEF是等腰直角三角形．           5分

（3 ）①当C、G重合时，如图4，

∵四边形ABCD是矩形，

∴∠A=∠ADC=90°，

∴∠AME+∠AEM=90°．

∵MG⊥EF，

∴∠EMG=90°．

∴∠AME+∠DMC=90°，

∴∠AEM=∠DMC，

∴△AEM∽△DMC

∴，

∴，

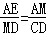∴AE=

当E、B重合时，AE最长为，

∴＜AE≤．        7分（注：此小问只需直接写出结果即可）

②如图3，△GEF是等边三角形．

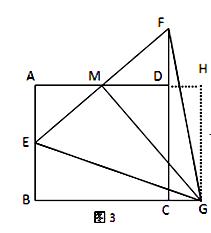
证明：过点G作GH⊥AD交AD延长线于点H，

∵∠A=∠B=∠AHG=90°，

∴四边形ABGH是矩形．

∴GH=AB=2．

∵MG⊥EF，

∴∠GME=90°．

∴∠AME+∠GMH=90°．

∵∠AME+∠AEM=90°，

∴∠AEM=∠GMH．

又∵∠A=∠GHM=90°，

∴△AEM∽△HMG．

∴．

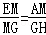在Rt△GME中，

∴tan∠MEG==．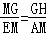

∴∠MEG=60°．

　由（1）得△AEM≌△DFM．

∴ME=MF．

∵MG⊥EF，  ∴GE=GF．

∴△GEF是等边三角形．           9分

考点：矩形的性质、三角形的全等与相似、等腰直角三角形、等边三角形、特殊三角函数值

点评：此题比较综合，四边形的相关性质和定理一般都由三角形性质和定理得来，故在解四边形时，通常会结合三角形的性质与定理帮助解题，难度适中。