
如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=θ1,∠PBA=θ2,∠PCB=θ3,∠PDC=θ4,若∠APB=80°,∠CPD=50°,则( )
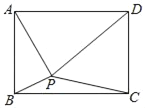
A. (θ1+θ4)﹣(θ2+θ3)=30° B. (θ2+θ4)﹣(θ1+θ3)=40°
C. (θ1+θ2)﹣(θ3+θ4)=70° D. (θ1+θ2)+(θ3+θ4)=180°
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源:2017-2018学年福建省三明市五县联考七年级(下)期末数学试卷 题型:填空题
冷冻一个20℃的物体,如果它每小时下降2℃,则物体的温度T(单位:℃)与冷冻时间t(单位:时)的关系式是____.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年河南省九年级(下)月考数学试卷(4月份) 题型:解答题
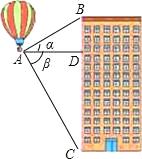
如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC.
查看答案和解析>>
科目:初中数学 来源:四川省南充市2018届中考模拟数学试卷 题型:解答题
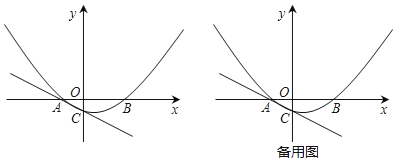
如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣ x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2018年中考数学模拟试卷(6月份) 题型:解答题
阅读下列材料,完成任务:
自相似图形
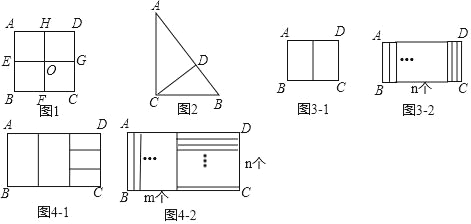
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).
查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级中考模拟数学试卷(6月份) 题型:单选题
已知二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象是( )
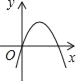
A.  B.
B. 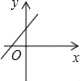 C.
C. 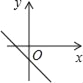 D.
D. 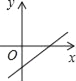
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com