练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数的图象如图所示，下列结论中，正确的结论的个数( )

    ①；②；③；④； ⑤．

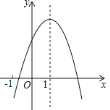
    A. 5个 B. 4个 C. 3个 D. 2个

    【答案】B

    【解析】

    根据x=1和x=-1时二次函数的值的情况进行推理，进而对所得结论进行判断①和②，由抛物线的开口方向、对称轴、抛物线与y轴的交点可以判断③、④、⑤.

    解：由图象可知，当x=1时，二次函数值为正，即a+b+c>0，故①正确；当x=-1时，二次函数值为负，即a-b+c<0，故②正确；图象开口向下，所以a<0，对称轴在y轴右侧，所以a与b异号，b>0，故⑤正确；抛物线与y轴交于正半轴，所以c>0，故abc<0，故③正确；对称轴为x=2，即，所以b=-4a，故④错误；所以正确的有①②③⑤.

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

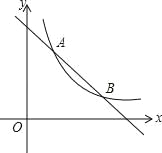
    【题目】如图，一次函数 y=﹣x+4 的图象与反比例 y=（k 为常数， 且 k≠0）的图象交于 A（1，a）、B（b，1）两点.

    （1）求点 A、B 的坐标及反比例函数的表达式；

    （2）在 x 轴上找一点，使 PA+PB 的值最小，求满足条件的点 P 的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，交于点，交于点，交于点，，，，给出下列结论：①；②；③；④；⑤.其中正确的结论有（ ）

    A.2个B.3个C.4个D.5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

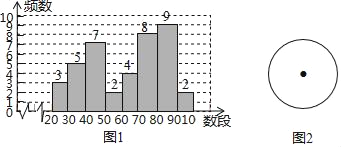
    【题目】某县九年级一模考试结束后，张老师依据一班考试成绩（单位：分）绘制了频数分布直方图（如图所示）

    根据频数分布直方图，解答下列问题．

    （1）填空：该班有_____人，根据直方图估算该班一模考试数学平均成绩是_____分；

    （2）请在所给半径为2的圆中，画出成绩在70≤x＜80的人数对应的扇形，并求出该扇形的面积；

    （3）从成绩在20≤x＜30和90≤x＜100的学生中任选2人，明明的成绩是91分，聪聪的成绩是28分，用树状图或列表法列出所有可能结果，并求明明、聪聪同时被选中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（知识重现）我们知道，在ax=N中，已知底数a，指数x，求幂N的运算叫做乘方运算．例如23=8；已知幂N，指数x，求底数a的运算叫做开方运算，例如=2；

    （学习新知）

    现定义：如果ax=N（a＞0且a≠1），即a的x次方等于N（a＞0且a≠1），那么数x叫做以a为底N的对数（logarithm），记作x=logaN．其中a叫做对数的底数，N叫做真数，x叫做以a为底N的对数．例如log28=3．零没有对数；在实数范围内，负数没有对数．

    （应用新知）

    （1）填空：在ax=N，已知幂N，底数a（a＞0且a≠1），求指数x的运算叫做_____运算；

    （2）选择题：在式子log5125中，真数是_____

    A.3 B.5 C.10 D.125

    （3）①计算以下各对数的值：log39；log327；log3243．

    ②根据①中计算结果，请你直接写出logaM，logaN，loga（MN）之间的关系．（其中a＞0且a≠1，M＞0，N＞0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们已经学习过多项式除以单项式，多项式除以多项式一般可用竖式计算，步骤如下：

    ①把被除式、除式按某个字母作降幂接列，井把所块的项用零补齐；

    ②用除式的第一项除以除式第一项，得到商式的第一项；

    ③用商式的一项去乘除式，把积写在被除式下面（同类项对齐），消去相等项；

    ④把减得的差当作新的被除式，再按照上面的方法继续演算，直到余式为零或余式的次数低于除式的次数时为止，被除式＝除式×商式+余式，若余式为零，说明这个多项式能被另一个多项式整除．

    例如：计算（6x4﹣7x3﹣x2﹣1）÷（2x+1），可用竖式除法如图：

    所以6x4﹣7x3﹣x2﹣1除以2x+1，商式为3x3﹣5x2﹣2x﹣1，余式为0．

    根据阅读材料，请回答下列问题：

    （1）（x3﹣4x2+7x﹣5）÷（x﹣2）的商是　 　，余式是　 　；

    （2）x3﹣x2+ax+b能被x2+2x+2整除，求a，b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

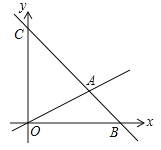
    【题目】如图，在平面直角坐标系中，过点的直线与直线相交于点，动点在线段和射线上运动．

    （1）求直线的解析式．

    （2）求的面积．

    （3）是否存在点，使的面积是的面积的？若存在求出此时点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，C，E为O上的两点，若AC平分∠EAB，CD⊥AE于点D．

    （1）求证：DC是⊙O切线；

    （2）若AO＝6，DC＝3，求DE的长；

    （3）过点C作CF⊥AB于F，如图2，若AD﹣OA＝1.5，AC＝3，求图中阴影部分面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从2019年9月1日起，我市积极开展垃圾分类活动，市环卫局准备购买、两种型号的垃圾箱，通过市场调研得知：购买3个型垃圾箱和2个型垃圾箱共需540元；购买2个型垃圾箱比购买3个型垃圾箱少用160元．

    （1）求每个型垃圾箱和型垃圾箱各多少元？

    （2）该市现需要购买、两种型号的垃圾箱共30个，设购买型垃圾箱个，购买型垃圾箱和型垃圾箱的总费用为元，求与的函数表达式，如果买型垃圾箱是型垃圾箱的2倍，求出购买型垃圾箱和型垃圾箱的总费用．

    查看答案和解析>>

    同步练习册答案