
已知双曲线y=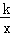 与直线y=
与直线y=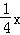 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=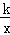 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线y=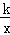 于点E,交BD于点C.
于点E,交BD于点C.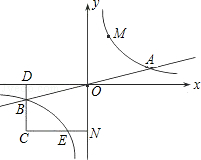
(1)若点D坐标是(﹣8,0),求A、B两点坐标及k的值;
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式;
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p﹣q的值.
(1)A(8,2) B(﹣8,﹣2) 16 (2)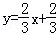 (3)-2
(3)-2
解析试题分析:(1)将D的坐标可得B的横坐标,代入解析式可得B的坐标,又有A、B两点关于原点对称,易得k的值;
(2)根据题意B是CD的中点,A、B、M、E四点均在双曲线上,可得BCD的坐标关于mn的表达式,进而可以表示出矩形的面积;代入数据可得答案;
(3)分别作AA1⊥x轴,MM1⊥x轴,垂足分别为A1、M1,设A点的横坐标为a,则B点的横坐标为﹣a,易得pq关于a的关系式,作p﹣q可得p﹣q=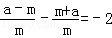 .
.
解:(1)∵D(﹣8,0),
∴B点的横坐标为﹣8,代入y=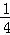 x中,得y=﹣2,
x中,得y=﹣2,
∴B点坐标为(﹣8,﹣2),
而A、B两点关于原点对称,∴A(8,2),
∴k=8×2=16;
(2)∵N(0,﹣n),B是CD的中点,A、B、M、E四点均在双曲线上,
∴mn=k,B(﹣2m,﹣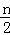 ),C(﹣2m,﹣n),E(﹣m,﹣n),
),C(﹣2m,﹣n),E(﹣m,﹣n),
∴S矩形DCNO=2mn=2k,
∴S△DBO=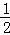 mn=
mn=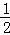 k,
k,
∴S△OEN=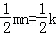 ,
,
∴S四边形OBCE=S矩形DCNO﹣S△DBO﹣S△OEN=k,
∴k=4,
由直线y=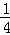 x及双曲线
x及双曲线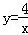 ,得A(4,1),B(﹣4,﹣1),
,得A(4,1),B(﹣4,﹣1),
∴C(﹣4,﹣2),M(2,2),
设直线CM的解析式是y=ax+b,
由C、M两点在这条直线上,得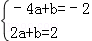 ,
,
解得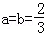 ,
,
∴直线CM的解析式是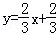 ;
;
(3)如图1,分别作AA1⊥x轴,MM1⊥x轴,垂足分别为A1、M1,
设A点的横坐标为a,则B点的横坐标为﹣a,
于是p=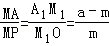 ,
,
同理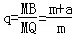 ,
,
∴p﹣q= .
.
本题也可用相似求解,如图,酌情给分.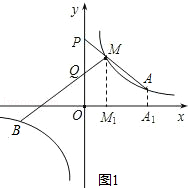
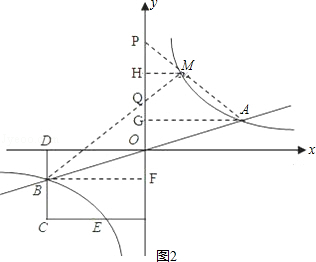
考点:反比例函数综合题.
点评:此题综合考查了反比例函数,正比例函数等多个知识点此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源:第5章《反比例函数》中考题集(24):3、反比例函数的应用(解析版) 题型:解答题
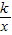 与直线y=
与直线y=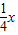 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=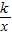 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=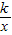 于点E,交BD于点C.
于点E,交BD于点C.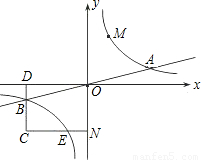
查看答案和解析>>
科目:初中数学 来源:2008-2009学年浙江省湖州市白雀学校九年级(上)期中数学试卷(解析版) 题型:填空题
 与直线y=
与直线y= 相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=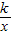 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=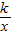 于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
查看答案和解析>>
科目:初中数学 来源:2012年广东省广州市聚贤暨四中中考数学一模试卷(解析版) 题型:解答题
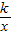 与直线y=
与直线y=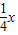 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=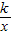 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=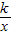 于点E,交BD于点C.
于点E,交BD于点C.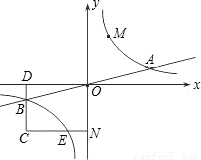
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《反比例函数》(05)(解析版) 题型:解答题
 与直线y=
与直线y=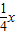 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=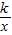 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=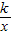 于点E,交BD于点C.
于点E,交BD于点C.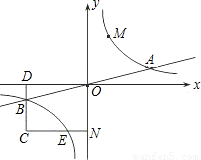
查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(16)(解析版) 题型:解答题
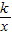 与直线y=
与直线y=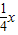 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=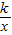 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=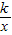 于点E,交BD于点C.
于点E,交BD于点C.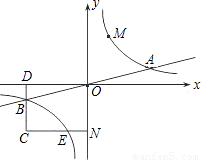
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com