
| A校 | B校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | 20 | 0.15 | 10 | 0.15 |
| 乙地 | 15 | 0.20 | 20 | 0.20 |

| A校 | B校 | |
| 甲地 | 1500 | 2000 |
| 乙地 | 2100 | 400 |
| A校 | B校 | |
| 甲地 | 1100 | 2400 |
| 乙地 | 2500 |
| 分数段 | 0~4 | 5~8 | 9~12 | 13~16 | 17~20 |
| 等级 | E | D | C | B | A |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年浙江省丽水市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《图形的相似》(05)(解析版) 题型:解答题
 与半径R、r之间的关系式,请证明你的结论;
与半径R、r之间的关系式,请证明你的结论;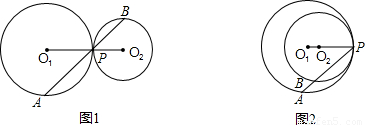
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《圆》(13)(解析版) 题型:解答题
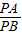 与半径R、r之间的关系式,请证明你的结论;
与半径R、r之间的关系式,请证明你的结论;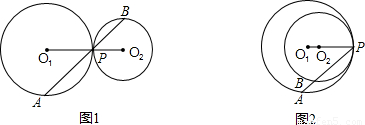
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《一元二次方程》(05)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com