练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知k=$\frac{c}{a+b}$=$\frac{b}{a+c}$=$\frac{a}{b+c}$，则y=kx-k一定经过第（　　）象限．
    A．一、二B．一、三C．一、四D．三、四

    分析 由k=$\frac{c}{a+b}$=$\frac{b}{a+c}$=$\frac{a}{b+c}$，得a=bk+ck，b=ak+ck，c=ak+bk，三式相加，求得k，从而得出答案．

    解答 解：1）当a+b+c=0时，b+c=-a，
    ∴k=$\frac{a}{b+c}$=-1，则直线是：y=-x+1，则经过一、二，四象限；
    2）当a+b+c≠0时，k=$\frac{a+b+c}{2（a+b+c）}$=$\frac{1}{2}$，
    则直线是：y=$\frac{1}{2}$x-$\frac{1}{2}$，一定经过第一、三、四象限
    ∴直线y=kx+2k一定经过第一、四象限．
    故选C．

    点评 本题考查了一次函数的性质和比例的性质，是基础知识比较简单．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图，△ABC中，∠ACB=90°，点E在BC上，以CE为直径的⊙O交AB于点F，AO∥EF
    （1）求证：AB是⊙O的切线；
    （2）如图2，连结CF交AO于点G，交AE于点P，若BE=2，BF=4，求$\frac{AP}{PE}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，已知△ABC的∠ABC和∠ACB的平分线BE，CF交于点G，若∠BGC=3∠A，则∠A=36°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

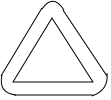    11．如图，在一三角形地块的四周种植宽度均为1m的草坪，外围三角均是以地块顶点为圆心的圆弧，并与各边通过相切连接，已知该三角形地块的周长为600m，则草坪外围的周长为（600+2π）m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．已知点（a，a）a≠0，给出下列变换：
    ①关于x轴轴对称；
    ②关于直线y=-x轴对称；
    ③关于原点中心对称．
    其中通过变换能得到坐标为（-a，-a）的变换是（　　）
    A．①②B．②③C．③D．①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若三角形三个内角度数的比为1：2：3，则这个三角形的最小角是（　　）
    A．15°B．30°C．45°D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列条件：①∠A+∠B=∠C；②∠A：∠B：∠C=3：4：5；③∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C；④∠A=∠B=2∠C；⑤∠A=∠B=$\frac{1}{2}$∠C，其中能确定△ABC为直角三角形的条件有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（m，2$\sqrt{2}$），B（3$\sqrt{2}$，0），C（n，-2$\sqrt{2}$），AC经过原点O，BH⊥AC于H，则AC•BH的值为24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．大正方体的体积为125cm3，小正方体的体积为8cm3，如图那样叠放在一起，这个物体的最高点A离地面的距离是7cm．

    查看答案和解析>>

    同步练习册答案