图形可以帮助刻画和描述问题；图形可以帮助发现和寻找解决问题的思路；图形可以帮助表述和记忆一些结果．积累一些图形模块，在类比发现中你会体验到问题解决的轻松，看图想事，看图说理一定会让你受益匪浅！
【探索与发现】
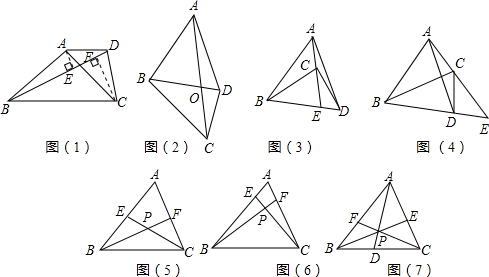
如图（1），梯形ABCD中，AD∥BC，对角线AC、BD相交于点O．则
=成立吗？试说明理由．
【思路与分析】
过点A作AE⊥BD于点E，过点C作CF⊥BD于点F．由于△ABD与△BCD同底不同高，所以二者的面积比可以转化为对应高的比；容易得到△AOE∽△COF，从而据相似三角形的性质，借助等量
的代换，
=成立．如图（2），对于四边形ABCD，
=的结论是否正确？试说明理由．
【应用与综合】
图（2）中的四边形ABCD沿BD边对折，连接并延长AC交BD（或其延长线）于点E，图（3）和图（4）是由此可能得到的情形：
在图（3）的情形下，试比较大小：
；（用“＞”或“＜”或“=”填空）
在图（4）的情形下，试比较大小：
；（用“＞”或“＜”或“=”填空）
【拓展与延伸】
（1）如图（5），E、F分别是△ABC两边AB、AC的中点，线段BF、CE相交于点P，则
=
；
（2）如图（6），E、F分别是△ABC两边AB、AC上的点，且 AE=mEB，AF=nFC，线段BF、CE相交于点P，则
=
．
（3）如图（7），在△ABC内任取一点P，连接并延长AP、BP、CP，分别交对边于点D、E、F，则
++=
．
如图，身高1.6米的小明从距路灯的底部（点O）20米的点A沿AO方向行走14米到点C处，小明在A处，头顶B在路灯投影下形成的影子在M处．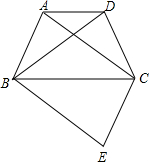
如图，四边形ABCD为等腰梯形，AD∥BC，连结AC、BD．在平面内将△DBC沿BC翻折得到△EBC．
