(0,2

)、(0,2)、(0,

)、(0,8)
分析:设P点坐标为(a,b),a>0,讨论:(1)若∠OQP=90°,①当∠POQ=30°,根据含30°的直角三角形三边的关系可得b=

a,而点P在反比例函数图象上,则

=b,得到

=

a,可解得a=2,则b=2

,于是可确定Q点坐标;②当∠OPQ=30°,利用同样方法可求Q点坐标;若∠OPQ=90°,作PA⊥y轴于A点,①当∠POQ=30°,根据(1)可得到P点坐标为(2,2

),再计算AQ的长,即可得到Q点坐标;②当∠PQO=30°,计算方法与②一样.
解答:设P点坐标为(a,b),a>0,
(1)若∠OQP=90°,
①当∠POQ=30°,则b=

a,
∵

=b,
∴

=

a,解得a=2,则b=2

,
∴Q点坐标为(0,2

),
②当∠OPQ=30°,则a=

b,
∵

=b,
∴

=

,解得a=2

,则b=2,
∴Q点坐标为(0,2);
(2)若∠OPQ=90°,
作PA⊥y轴于A点,如图,
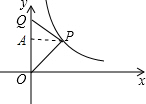
①当∠POQ=30°,则b=

a,
∵

=b,
∴

=

a,解得a=2,则b=2

,
∴P点坐标为(2,2

),
∵∠QPA=30°,
∴AQ=

AP=

,
∴OQ=2

+

=

,
∴Q点坐标为(0,

);
②当∠PQO=30°,则a=

b,
∵

=b,
∴

=

,解得a=2

,则b=2,
∴P点坐标为(2

,2);
∵∠PQA=30°,
∴AQ=

AP=6,
∴OQ=6+2=8,
∴Q点的坐标为(0,8).
∴符合条件的点Q的坐标为(0,2

)、(0,2)、(0,

)、(0,8).
故答案为(0,2

)、(0,2)、(0,

)、(0,8).
点评:本题考查了反比例函数的综合题:反比例函数y=

图象上的点满足其解析式;利用含30°的直角三角形三边的关系可简化计算;运用分类讨论的思想使解题更加完整.

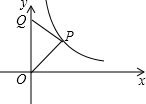 如图,点P是双曲线
如图,点P是双曲线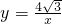 (x>0)上动点,在y轴上取点Q,使得以P、Q、O 为顶点的三角形是含有30°角的直角三角形,则符合条件的点Q的坐标是________.
(x>0)上动点,在y轴上取点Q,使得以P、Q、O 为顶点的三角形是含有30°角的直角三角形,则符合条件的点Q的坐标是________. )、(0,2)、(0,
)、(0,2)、(0, )、(0,8)
)、(0,8) a,而点P在反比例函数图象上,则
a,而点P在反比例函数图象上,则 =b,得到
=b,得到 =
= a,可解得a=2,则b=2
a,可解得a=2,则b=2 ,于是可确定Q点坐标;②当∠OPQ=30°,利用同样方法可求Q点坐标;若∠OPQ=90°,作PA⊥y轴于A点,①当∠POQ=30°,根据(1)可得到P点坐标为(2,2
,于是可确定Q点坐标;②当∠OPQ=30°,利用同样方法可求Q点坐标;若∠OPQ=90°,作PA⊥y轴于A点,①当∠POQ=30°,根据(1)可得到P点坐标为(2,2 ),再计算AQ的长,即可得到Q点坐标;②当∠PQO=30°,计算方法与②一样.
),再计算AQ的长,即可得到Q点坐标;②当∠PQO=30°,计算方法与②一样. a,
a, =b,
=b, =
= a,解得a=2,则b=2
a,解得a=2,则b=2 ,
, ),
), b,
b, =b,
=b, =
= ,解得a=2
,解得a=2 ,则b=2,
,则b=2,
 a,
a, =b,
=b, =
= a,解得a=2,则b=2
a,解得a=2,则b=2 ,
, ),
), AP=
AP= ,
, +
+ =
= ,
, );
); b,
b, =b,
=b, =
= ,解得a=2
,解得a=2 ,则b=2,
,则b=2, ,2);
,2); AP=6,
AP=6, )、(0,2)、(0,
)、(0,2)、(0, )、(0,8).
)、(0,8). )、(0,2)、(0,
)、(0,2)、(0, )、(0,8).
)、(0,8). 图象上的点满足其解析式;利用含30°的直角三角形三边的关系可简化计算;运用分类讨论的思想使解题更加完整.
图象上的点满足其解析式;利用含30°的直角三角形三边的关系可简化计算;运用分类讨论的思想使解题更加完整. 

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案 如图,点A是双曲线y=
如图,点A是双曲线y= (2013•萧山区模拟)如图,点P是双曲线y=
(2013•萧山区模拟)如图,点P是双曲线y= (2013•南通二模)如图,点A是双曲线y=
(2013•南通二模)如图,点A是双曲线y= 如图,点M是双曲线y=
如图,点M是双曲线y=