在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P在斜边AB上,且CP2=AP•BP,则CP的长为________.
2.5或2.4
分析:首先设AP=x,然后表示出BP=5-x,利用已知的等积式得到CP
2=x(5-x),然后在△ACP中,根据余弦定理得到CP
2=AC
2+AP
2-2AC•APcosA=9+x
2-6x×0.6,从而得到有关x的方程9+x
2-6x•0.6=x(5-x)解之即可.
解答:设AP=x,则BP=5-x,CP
2=x(5-x)
在△ACP中,根据余弦定理有
CP
2=AC
2+AP
2-2AC•APcosA=9+x
2-6x×0.6
则有9+x
2-6x•0.6=x(5-x)
整理,得10x
2-43x+45=(2x-5)(5x-9)=0
解得:x=2.5或x=1.8
所以CP=2.5或CP=
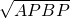
=
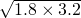
=2.4,
故答案为2.5或2.4.
点评:本题考查了相似三角形的判定与性质,初中教材中已经将余弦定理的内容删掉,解题是可以借助网络等渠道了解余弦定理.

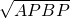 =
=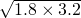 =2.4,
=2.4,

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案