
 C2的坐标;
C2的坐标; 解:(1)∵A(0,0),B(6,0),C(5,5),
解:(1)∵A(0,0),B(6,0),C(5,5), ×6×5=15;
×6×5=15;

科目:初中数学 来源: 题型:
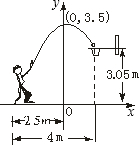 如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.建立如图所示的直角坐标系,则抛物线的表达式为
如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.建立如图所示的直角坐标系,则抛物线的表达式为查看答案和解析>>
科目:初中数学 来源: 题型:
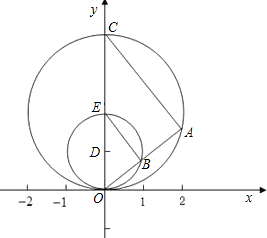 角形?若存在,求出点P的坐标;若不存在,说明其理由.
角形?若存在,求出点P的坐标;若不存在,说明其理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在边长为1的方格纸上建立如图所示的直角坐标系,把△ABC向下平移6个单位长度,得到△A1B1C1,画从出△A1B1C1,并作出△A1B1C1关于y轴对称的△A2B2C2,并直接写出点A2,B2,C2的坐标.
18、在边长为1的方格纸上建立如图所示的直角坐标系,把△ABC向下平移6个单位长度,得到△A1B1C1,画从出△A1B1C1,并作出△A1B1C1关于y轴对称的△A2B2C2,并直接写出点A2,B2,C2的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com