
 新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:
新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:分析 (1)根据每个作业本1.5元或2元计算费用;
(2)根据直方图解答;
(3)根据平均数的计算方法解答.
解答 解:(1)当x≤18时,y=18×1.5=27(元).
当x>18时,y=18×1.5+2(x-18)=2x-9;
(2)如图,使用16个作业本有2人,频率为:$\frac{2}{30}$.
使用17个作业本有6人,频率为:$\frac{6}{30}$.
使用10个作业本有2人,频率为:$\frac{10}{30}$.
∵$\frac{2}{30}$+$\frac{6}{30}$=$\frac{8}{30}$<0.5,
$\frac{2}{30}$+$\frac{6}{30}$+$\frac{10}{30}$=0.6>0.5,
∴最少购买18个作业本;
(3)$\overline{x}$=$\frac{1}{30}$[16×1.5×2+17×1.5×6+18×1
.5×10+18×1.5×8+18×1.5×4+(19-18)×2+(20-18)×2]=26.7(元).
答:这30名学生平均使用作业本的费用为26.7元.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
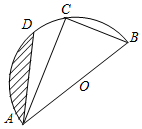 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a0=1 | B. | $\sqrt{32}$-$\sqrt{8}$=2$\sqrt{2}$ | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{18}$÷2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形OABC的边OA、OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA、OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com