
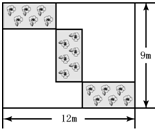
 列方程(组)解应用题.
列方程(组)解应用题.
|
|
|
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
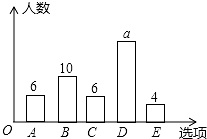 为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该调查的调查方式及图中a的值分别是( )
为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该调查的调查方式及图中a的值分别是( )| A、全面调查;26 |
| B、全面调查;24 |
| C、抽样调查;26 |
| D、抽样调查;24 |
查看答案和解析>>
科目:初中数学 来源: 题型:
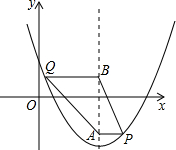 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com