
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
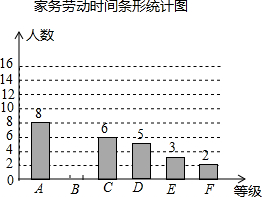 某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:
某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分A、B、C、D、E、F六个等级,绘制了如图所示的不完整的统计图表:| 等级 | 家务劳动时间 (分钟) | 人数 | 百分比 |
| A | 50以上 | 8 | 20% |
| B | 41-50 | a | 40% |
| C | 31-40 | 6 | 15% |
| D | 21-30 | 5 | 12.5% |
| E | 11-20 | 3 | 7.5% |
| F | 0-10 | 2 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
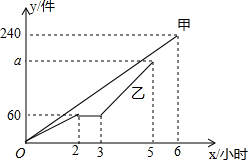 甲、乙两组工人同时开始加工某种零件,乙组在工作2小时后停产1小时更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与开工后时间x(时)之间的函数图象如图1所示.
甲、乙两组工人同时开始加工某种零件,乙组在工作2小时后停产1小时更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与开工后时间x(时)之间的函数图象如图1所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
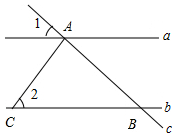 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=44°,则∠2的度数是( )
如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=44°,则∠2的度数是( )| A. | 36° | B. | 44° | C. | 46° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
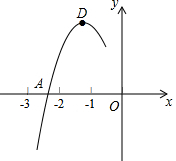 抛物线y=ax2+bx+c的顶点D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c>0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.
抛物线y=ax2+bx+c的顶点D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c>0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.| A. | ③④ | B. | ②④ | C. | ②③ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com