
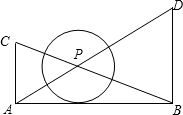
 如图,∠CAB=∠ABD=90°,AB=AC+BD,AD交BC于P,作⊙P与AB相切.
如图,∠CAB=∠ABD=90°,AB=AC+BD,AD交BC于P,作⊙P与AB相切.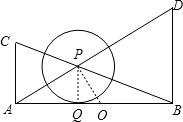 解:⊙O与⊙P相内切.
解:⊙O与⊙P相内切.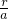 =
=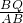 ,
, =
=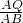 ,
,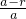 =
= ,
, ,
, ,
,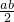 ,
,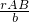 =
=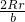 =a,
=a, -a=
-a=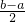 ,
,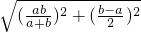 =
=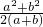 =
= -
- =R-r.
=R-r.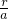 =
=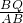 ,
, =
=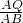 ,故可求得r的值;然后⊙O的半径R=
,故可求得r的值;然后⊙O的半径R= ,⊙P的半径为r=
,⊙P的半径为r= ,可得到AQ=
,可得到AQ=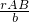 =
=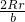 =a,OQ=
=a,OQ= -a=
-a=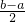 ,连接PO,由勾股定理得到PO=R-r,故⊙O与⊙P相内切.
,连接PO,由勾股定理得到PO=R-r,故⊙O与⊙P相内切.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com