
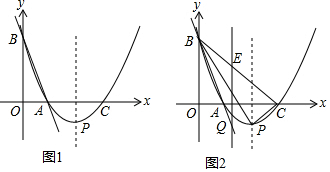
 等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.
等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.分析 (1)先配成两个完全平方式的和等于0,从而求出a,b即可得出点A,C坐标;
(2)由点A,C坐标求出直线AC解析式,由等腰直角三角形的性质即可得出点B坐标;
(3)利用点的坐标和互相垂直的直线的斜率互为负倒数,分别求出点F,E,G的坐标,最后求出CG,CE,AE,即可找出关系式.
解答 解:(1)∵a2+b2-4a-10b+29=0.
∴(a-2)2+(b-5)2=0,
∴a=2,b=5,
∴A(0,2),C(5,0),
(2)∵△ABC是等腰直角三角形,
∴AB⊥AC,AB=AC,
由(1)知,A(0,2),C(5,0),
∴AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{29}$,
∴直线AC解析式为y=-$\frac{2}{5}$x+2,
∴直线AB解析式为y=$\frac{5}{2}$x+2,
∴设点B(m,$\frac{5}{2}$m+2),
∴AB=$\sqrt{{m}^{2}+(\frac{5}{2}m+2-2)^{2}}$=$\sqrt{29}$,
∴m=2(舍)或m=-2,
∴B(-2,-3),
(3)由(2)知,直线AB解析式为y=$\frac{5}{2}$x+2,
∴D(-$\frac{4}{5}$,0),
∴AD2=$\frac{16}{25}$+4=$\frac{116}{25}$,
∵B(-2,-3),C(5,0),
∴直线BC解析式为y=$\frac{3}{7}$x-$\frac{15}{7}$,
∴E(0,-$\frac{15}{7}$),
由(2)知,直线AC解析式为y=-$\frac{2}{5}$x+2,∴
设F(n,-$\frac{2}{5}$n+2),
∴AF2=n2+($\frac{2}{5}$n)2=$\frac{29}{25}$n2,
∵AD=AF,
∴$\frac{29}{25}$n2=$\frac{116}{25}$,
∴n=-2(舍)或n=2,
∴F(2,$\frac{6}{5}$),
∵B(-2,-3),
∴直线BF解析式为y=$\frac{21}{20}$x-$\frac{9}{10}$,
∵EG⊥BF,E(0.-$\frac{15}{7}$),
∴直线EG解析式为y=-$\frac{20}{21}$x-$\frac{15}{7}$,
∴G(-$\frac{9}{4}$,0),
∴CG=$\frac{29}{4}$,EG=$\frac{3×39}{28}$,
∵AE=$\frac{29}{7}$,
∴CG=EG+AE.
点评 此题是三角形综合题,主要考查等腰直角三角形的性质,待定系数法,平面坐标系内,两点间的距离公式,解本题的关键是用代数的方法解决几何问题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:单选题
如图,将△AB C沿AB方向向右平移得到△DEF,其中AF=8,DB=2,则平移的距离为( )
C沿AB方向向右平移得到△DEF,其中AF=8,DB=2,则平移的距离为( )
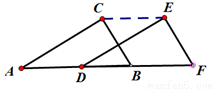
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
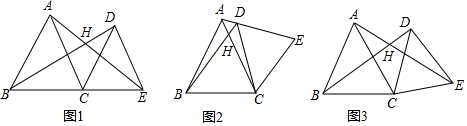
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图Rt△ABC的外接圆⊙O,∠ACB=90°,∠ACB的平分线交⊙O于D.
如图Rt△ABC的外接圆⊙O,∠ACB=90°,∠ACB的平分线交⊙O于D.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图所示的图案分别是大众、三菱、奔驰、奥迪汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com