
 在Rt△ABC中,∠A=90°,tanB=
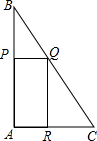
在Rt△ABC中,∠A=90°,tanB= ,点P在线段AB上运动,点Q、R分别在线段BC,AC上,且使得四边形APQR是矩形.设AP的长是x,矩形APQR面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线上的一部分.
,点P在线段AB上运动,点Q、R分别在线段BC,AC上,且使得四边形APQR是矩形.设AP的长是x,矩形APQR面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线上的一部分. ,
, =
= ,
, ,
, =
= ,
, x,AR=AC-
x,AR=AC- x,
x, ),把(12,36)代入得:12(AC-
),把(12,36)代入得:12(AC- ×12)=36,
×12)=36, x2+12x,
x2+12x, =8时,函数值最大,最大值是:-
=8时,函数值最大,最大值是:- ×82+12×8=48.
×82+12×8=48.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com