
【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.

求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
【答案】(1)A地购买了400吨原料,制成运往B地的产品300吨(2)1887800元
【解析】
解:(1)设工厂从A地购买了x吨原料,制成运往B地的产品y吨,
依题意得:![]() ,整理得:
,整理得:![]() ,
,
①×12-②得:13y=3900,解得:y=300。
将y=300代入①得:x=400,
∴方程组的解为:![]() 。
。
答:工厂从A地购买了400吨原料,制成运往B地的产品300吨。
(2)依题意得:300×8000-400×1000-15000-97200=1887800(元),
∴这批产品的销售款比原料费与运输费的和多1887800元。
(1)设工厂从A地购买了x吨原料,制成运往B地的产品y吨,利用两个等量关系:A地到长青化工厂的公路里程×1.5x+B地到长青化工厂的公路里程×1.5y=这两次运输共支出公路运输费15000元;A地到长青化工厂的铁路里程×1.2x+B地到长青化工厂的铁路里程×1.2y=这两次运输共支出铁路运输费97200元,列出关于x与y的二元一次方程组,求出方程组的解集得到x与y的值,即可得到该工厂从A地购买原料的吨数以及制成运往B地的产品的吨数。
(2)由第一问求出的原料吨数×每吨1000元求出原料费,再由这两次运输共支出公路运输费15000元,铁路运输费97200元,两运费相加求出运输费之和,由制成运往B地的产品的吨数×每吨8000元求出销售款,最后由这批产品的销售款-原料费-运输费的和,即可求出所求的结果。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15o,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM。则下列结论:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分AB;④ME=BD;正确的有( )
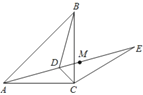
A. 1个B. 4个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
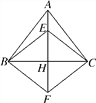
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,则下列四个结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1 , 作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1 , 它的面积记作S2 , 照此规律作下去,则S1= , S2017= . 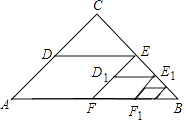
查看答案和解析>>
科目:初中数学 来源: 题型:
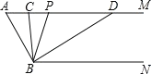
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上的动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画 ![]() ,连结AF,CF,则图中阴影部分面积为 .
,连结AF,CF,则图中阴影部分面积为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com