
如图①,用塑料制成的密封三棱柱的筒里装有一定量的水,图②是它的平面展开图.现在把这个筒的EFGH面作为底面,放在水平桌面上,水面的高度是2 cm.



(1)求矩形EFGH的宽FG;
(2)把△DME面(直角三角形面)作为底面(如图③)放在水平桌面上,求水面的高.
科目:初中数学 来源:2013届江苏省无锡市宜兴实验学校九年级5月中考适应性考试数学试卷(带解析) 题型:填空题
已知:图1是一块学生用直角三角板,其中∠A′=30°,三角板的边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).将直径为4cm的⊙O移向三角板,三角板的内ABC的斜边AB恰好等于⊙O的直径,它的外△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2),则边B′C′的长为 cm.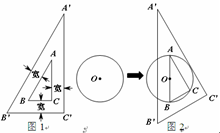
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省无锡市宜兴九年级5月中考适应性考试数学试卷(解析版) 题型:填空题
已知:图1是一块学生用直角三角板,其中∠A′=30°,三角板的边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).将直径为4cm的⊙O移向三角板,三角板的内ABC的斜边AB恰好等于⊙O的直径,它的外△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2),则边B′C′的长为 cm.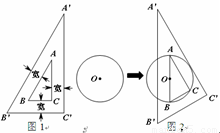
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com