练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如下图所示，四边形ABCD是正方形，对角线AC与BD相交于O，MN∥AB，且分别与AO，
    BO交于M、N，
    求证：（1）BM=CN；
                （2）BM⊥CN．
    证明：（1）∵MN∥AB，
    ∴∠OMN=∠ONM=∠OAB=∠OBA=45°，
    ∴AM=OA﹣OM=OB﹣ON=BN，
    在△ABM和△BCN中，
    ∵，
    ∴△ABM≌△BCN，
    ∴BM=CN．
    （2）由△ABM≌△BCN，得∠ABM=∠BCN，
    又∵∠ABM+∠CBM=90°，
    ∴∠BCN+∠CBM=90°，
    ∴CN⊥BM．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：新教材完全解读　七年级数学下册　人教版 人教版 题型：044

    如下图所示，四边形ABCD中，∠B＝90°，EF⊥AD，则∠A＝∠EFC，为什么？

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　下册(配北师大版新课标) 北师大版新课标 题型：022

    如下图所示，四边形ABCD内接于⊙O，∠BCD＝120°，则∠BOD＝________．

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　下册(配北师大版新课标) 北师大版新课标 题型：022

    如下图所示，四边形ABCD是正方形，曲线DA1B1C1D1…叫做“正方形的渐开线”，其中，…的圆心依次按A，B，C，D循环．取AB＝1，则曲线DA1B1…C2D2的长是________．(结果保留π)

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　下册(配北师大版新课标) 北师大版新课标 题型：044

    如下图所示，四边形ABCD内接于⊙O，∠B＝90°，∠DAB＝∠DCA．过点D作DP⊥AC于P，tan∠DAC＝，S△ACD＝8．

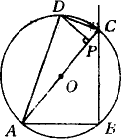
    (1)求DP的长；

    (2)求sin∠BAC的值．

    查看答案和解析>>

    同步练习册答案