
 已知:如图,直线y=-x+3与x轴、y轴交于点A,点B,点O关于直线AB的对称点为点O′,且点O′恰好在反比例函数y=$\frac{k}{x}$的图象上.
已知:如图,直线y=-x+3与x轴、y轴交于点A,点B,点O关于直线AB的对称点为点O′,且点O′恰好在反比例函数y=$\frac{k}{x}$的图象上.分析 (1)分别令直线y=-x+3中的x=0,y=0即可求得A、B两点的坐标;
(2)根据对称点的性质即可;
(3)分两种情况:①当点P在点B的上方时,即:m>3,延长AO′于PQ相交于点M,设P(0,m),由面积关系可求;②当点P在点B的上方时,即:0<m<3,方法同上.
解答 解:(1)A(3,0),B(0,3)
(2)如图①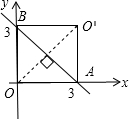
图①
∵点O与O′关于直线AB对称,
∴由题意可得四边形OAO′B为正方形,
∴O′(3,3)
则 k=3×3=9
即:k的值为9
(3)设P(0,m),显然,点P与点B不重合
①当点P在点B的上方时,即:m>3,
延长AO′于PQ相交于点M,如图②所示: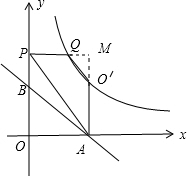
则:Q($\frac{9}{m}$,m),M(3,m)
∴PM=3,AM=m,MO′=m-3,QM=3-$\frac{9}{m}$,
∴S=S△PMA-S△QMO′=$\frac{3}{2}{S}_{△OAB}$=$\frac{3}{2}$×$\frac{9}{2}$=$\frac{27}{4}$
∴$\frac{3}{2}m$-$\frac{1}{2}$(3-m)(m+3)=$\frac{27}{4}$,
解之得:m=6
②当点P在点B的上方时,即:0<m<3,如图③所示: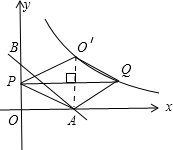
显然,PQ⊥AO′,
∴S=$\frac{1}{2}$•PQ•AO′=$\frac{1}{2}$×3×$\frac{9}{m}$=$\frac{27}{4}$,
∴m=2
∴P(0,2)或(0,6)
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是理解函数图象与坐标轴的交点的实质、对称点的性质及综合分析问题的能力.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必过点(0,0) | |
| B. | 直线与坐标轴围成的三角形的面积为0.5 | |
| C. | 图象经过第一、二、三象限 | |
| D. | y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 正方形的边长依次为2,4,6,8,…,它们在直角坐标系中的位置如图所示,其中A1(1,1),A2(-1,1),A3(-1,-1),A4(1,-1),A5(2,2),A6(-2,2),A7(-2,-2),A8(2,-2),A9(3,3),A10(-3,3),…,按此规律排下去,则A2016的坐标为( )
正方形的边长依次为2,4,6,8,…,它们在直角坐标系中的位置如图所示,其中A1(1,1),A2(-1,1),A3(-1,-1),A4(1,-1),A5(2,2),A6(-2,2),A7(-2,-2),A8(2,-2),A9(3,3),A10(-3,3),…,按此规律排下去,则A2016的坐标为( )| A. | (504,-504) | B. | (-504,-504) | C. | (-504,504) | D. | (504,504) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有最小值,且最小值为1 | B. | 有最大值,且最大值为3 | ||
| C. | 有最大值,且最大值为1 | D. | 有最小值,且最小值为3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com