
����Ŀ����֪��������A��B��C���㣬�ֱ������24����10��10����ֻ�������ϼס��ҷֱ��A��C����ͬʱ������У����ٶ�Ϊ4����λ/��,�ҵ��ٶ�Ϊ6����λ/�롣
��1���ס��Ҷ������������
��2���׳����������A��B��C����ľ����Ϊ40����λ��
��3������A��B��C����ľ����Ϊ40����λʱ����ͷԭ�ٷ��أ����ס������������ٴ�����ʱ���������ʾ������____________.
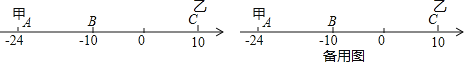
���𰸡�3.4s��
����������1������x�����������������ݼ����ҵ�·�̲�Ϊ34�����г�������⼴�ɣ�
��2����y����A��B��C����ľ���֮��Ϊ40����λ���ּ�ӦΪ��AB��BC֮������������ۼ�����⣻
��3��������������ټ״�A�����˶�2��ʱ���أ���y�����������. ��ʱ�ס��ұ�ʾ��������Ϊͬһ�㣬����ʾ������ͬ.�ڼ״�A�����˶�5��ʱ���أ���y��������������������ۼ������.
�⣺��1����xs�����������
4x+6x=34��
��ã�x=3.4s��
��2��4��3.4=13.6��-24+13.6=-10.4
�ʼס����������ϵ�-10.4������
��3����y����A��B��C����ľ���֮��Ϊ40����λ��
B���A��C����ľ���Ϊ14+20=34��40��A���B��C����ľ���Ϊ14+34=48��40��C���A��B�ľ���Ϊ34+20=54��40���ʼ�ӦΪ��AB��BC֮�䣮
��AB֮��ʱ��4y+��14-4y��+��14-4y+20��=40
���y=2��
��BC֮��ʱ��4y+��4y-14��+��34-4y��=40��
���y=5��
��3���ټ״�A�����˶�2��ʱ���أ���y���������������ʱ�ס��ұ�ʾ��������Ϊͬһ�㣬����ʾ������ͬ��
�ױ�ʾ����Ϊ��-24+4��2-4y���ұ�ʾ����Ϊ��10-6��2-6y��
��������ã�-24+4��2-4y=10-6��2-6y��
��ã�y=7��
�������ʾ����Ϊ��-24+4��2-4y=-44����10-6��2-6y=-44����
�ڼ״�A�����˶�5��ʱ���أ���y�������������
�ױ�ʾ����Ϊ��-24+4��5-4y���ұ�ʾ����Ϊ��10-6��5-6y��
��������ã�-24+4��5-4y=10-6��5-6y��
��ã�y=-8������������ȥ����
���״�A�����˶�2��ʱ���أ����������������������������ʾ����Ϊ-44��
���㾦��������һԪһ�η��̵�Ӧ�ã�����ؼ���Ҫ������Ŀ����˼��������Ŀ�������������ҳ����ʵĵ�����ϵ�г����̣�����⣮�����ڽ��ڣ�3����ע�����˼������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x=1�Ƿ���x2��2x+c=0��һ��������ʵ��c��ֵ�ǣ�������
A. ��1 B. 0 C. 1 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����40cm�������ܷ�Χ��һ�����Ϊ110cm2�ľ��Σ����ܣ�˵��Χ����������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x=1�Ƕ��η��̣�m2��1��x2��mx+m2=0��һ��������ôm��ֵ�ǣ�������
A. 0.5��1 B. ��0.5 C. 0.5�� 1 D. 0.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������E��![]() �ϵ�һ�㣬��DBC=��BED��
�ϵ�һ�㣬��DBC=��BED��
��1����֤��BC�ǡ�O�����ߣ�
��2����֪AD=3��CD=2����BC�ij���
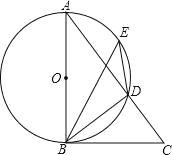
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x2��4x��12=0�Ľ�Ϊ��������
A. x1=2��x2=6 B. x1=2��x2=��6 C. x1=��2��x2=6 D. x1=��2��x2=��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���й��ɵ�ͼ�����������ɱ߳���ͬ��С��������ɣ����в���С������Ϳ����Ӱ�����˹��ɣ���n��ͼ������______��Ϳ����Ӱ��С�����Σ��ú���n�Ĵ���ʽ��ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90�㣬��ABC=60�㣬BC=2cm��DΪBC���е㣬������E��1cm/s���ٶȴ�A�����������A��B��A�ķ����˶�����E����˶�ʱ��Ϊt�루0��t��6��������DE������BDE��ֱ��������ʱ��t��ֵΪ�� ��
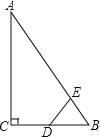
A��2B��2.5��3.5
C��3.5��4.5D��2��3.5��4.5
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com