
【题目】已知:关于x的一元二次方程kx2﹣(4k+1)x+3k+3=0(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求k的值.
【答案】(1)证明见解析(2)1或﹣1
【解析】
(1)根据一元二次方程的定义得k≠0,再计算判别式得到△=(2k-1)2,然后根据非负数的性质,即k的取值得到△>0,则可根据判别式的意义得到结论;(2)根据求根公式求出方程的根,方程的两个实数根都是整数,求出k的值.
(1)证明:△=[﹣(4k+1)]2﹣4k(3k+3)=(2k﹣1)2.
∵k为整数,
∴(2k﹣1)2>0,即△>0.
∴方程有两个不相等的实数根.
(2)解:∵方程kx2﹣(4k+1)x+3k+3=0为一元二次方程,
∴k≠0.
∵kx2﹣(4k+1)x+3k+3=0,即[kx﹣(k+1)](x﹣3)=0,
∴x1=3,![]() .
.
∵方程的两个实数根都是整数,且k为整数,
∴k=1或﹣1.


科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC. 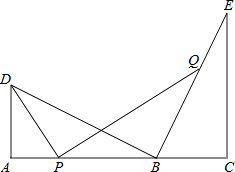
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q; (i)当点P与A、B两点不重合时,求 ![]() 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O,根据下列条件,求出∠BOC的度数.
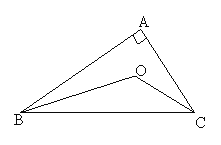
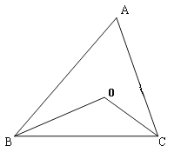
(1)已知∠ABC+∠ACB=100°,则∠BOC= .
(2)已知∠A=90°,求∠BOC的度数.
(3)从上述计算中,你能发现∠BOC与∠A的关系吗?请直接写出∠B0C与∠A的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33) 
查看答案和解析>>
科目:初中数学 来源: 题型:
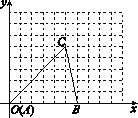
【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求三角形ABC的面积;
(2)如果三角形ABC的三个顶点的纵坐标不变,横坐标增加3个单位长度,得到三角形A1B1C1,试在图中画出三角形A1B1C1,并写出点A1,B1,C1的坐标;
(3)(2)中三角形A1B1C1与三角形ABC的大小、形状有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y= ![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( ) 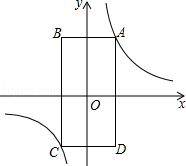
A.一直增大
B.一直减小
C.先增大后减小
D.先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
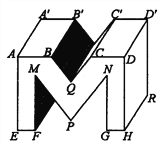
【题目】如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系?CC′与DH有何位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com