
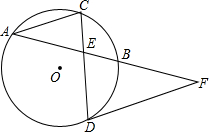
 如图,⊙O的弦AB、CD相交于点E,C为$\widehat{AB}$的中点,过D点作⊙O的切线交AB的延长线于点F.
如图,⊙O的弦AB、CD相交于点E,C为$\widehat{AB}$的中点,过D点作⊙O的切线交AB的延长线于点F.分析 (1)连接OC,OD,根据垂径定理得到OC⊥AB,求得∠OCE+∠CEA=∠OCE+∠FED=90°,由DF是⊙O的切线,得到OD⊥DF,得到∠ODC+∠EDF=90°,等量代换得到∠DEF=∠EDF,于是得到结论;
(2)如图,作辅助线;证明OH⊥AB,AH=4λ,此为解题的关键性结论;证明CE=$\sqrt{10}$;列出方程r2=(r-3λ)2+(4λ)2,求出λ=$\frac{6}{25}$r=2,即可解决问题.
解答 解:(1)连接OC,OD,
∵C为$\widehat{AB}$的中点,
∴OC⊥AB,
∴∠OCE+∠CEA=∠OCE+∠FED=90°,
∵DF是⊙O的切线,
∴OD⊥DF,
∴∠ODC+∠EDF=90°,
∵OC=OD,
∴∠OCD=∠ODC,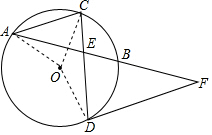
∴∠DEF=∠EDF,
∴EF=DF;
(2)如图,连接OA、OC;
由(1)知OC⊥AB,
∴AH=BH;
∵AC∥DF,
∴∠ACD=∠CDF;而EF=DF,
∴∠DEF=∠CDF=∠ACD,
∴AC=AE;
设AE=5λ,则BE=3λ,
∴AH=4λ,HE=λ,AC=AE=5λ;
∴由勾股定理得:CH=3λ;
CE2=CH2+HE2=9λ2+λ2,
∴CE=$\sqrt{10}$;
在直角△AOH中,由勾股定理得:
AO2=AH2+OH2,
即r2=(r-3λ)2+(4λ)2,
解得:λ=$\frac{6}{25}$r=$\frac{6}{25}$×$\frac{25}{3}$=2,
∴CE=2$\sqrt{10}$.
点评 该题主要考查了圆的切线的性质的应用问题,垂径定理,勾股定理,解题的关键是作辅助线;灵活运用有关定理来分析、解答.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 295 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.
如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com