
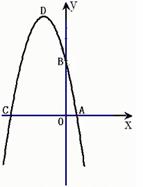
如图, 抛物线![]() 与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程
与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程![]() 的两个实数根.
的两个实数根.
(1)求A、B两点的坐标;
(2) 求出此抛物线的的解析式及顶点D的坐标;
(3)求出此抛物线与x轴的另一个交点C的坐标;
(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由.
解:(1)∵![]() 的两个实数根为
的两个实数根为![]()
OA、OB(OA<OB)的长是方程![]() 的两个实数根
的两个实数根
∴ OA=1,OB=5
∴ A(1,0), B(0,5)
(2)∵抛物线![]() 与x轴的一个交点是A,与y轴的交点是B
与x轴的一个交点是A,与y轴的交点是B
∴![]()
解得:![]()
∴所求二次函数的解析式为:![]() -
-
顶点坐标为:D(-2,9)
(3)此抛物线与x轴的另一个交点C的坐标为(-5,0)
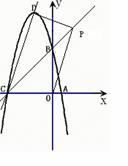 (4)直线CD的解析式为:
(4)直线CD的解析式为:
y=3x+15
直线BC的解析式为:
y=x+5
①若以CD为底,则OP∥CD
直线OP的解析式为:y=3x
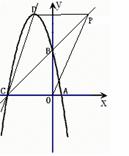 于是有
于是有![]() 解得:
解得: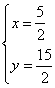
∴点P的坐标为(![]()
②若以OC为底,则DP∥CO
直线DP的解析式为:y=9
于是有![]() 解得:
解得:![]()
∴点P的坐标为(4,9)
∴在直线BC上存在点P,使四边形PDCO为梯形且P点坐标为(![]() 或
或
(4,9)


科目:初中数学 来源:四川省中考真题 题型:解答题
 与x轴交于A、B两点,与y轴交于点C(0,-1),且对称轴x=1。
与x轴交于A、B两点,与y轴交于点C(0,-1),且对称轴x=1。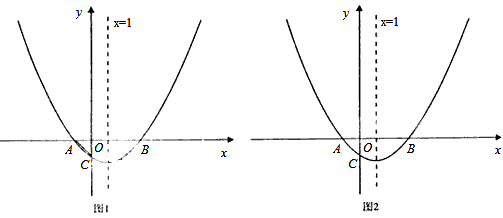
查看答案和解析>>
科目:初中数学 来源: 题型:
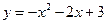 与x轴相交于点A和点B,与y轴交于点C.
与x轴相交于点A和点B,与y轴交于点C. =6,求点M的坐标.
=6,求点M的坐标.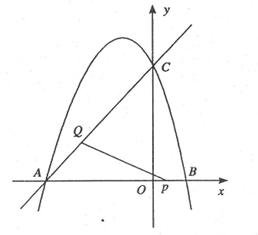
查看答案和解析>>
科目:初中数学 来源: 题型:
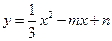 与x轴交于A、B两点,与y轴交于点C(0.
与x轴交于A、B两点,与y轴交于点C(0. ).且对称抽x=l.
).且对称抽x=l.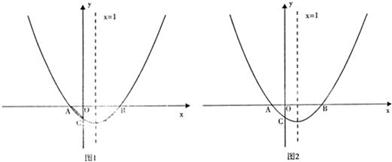
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川广安卷)数学 题型:解答题
如图抛物线 与x轴交于A、B两点,与y轴交于点C(0.
与x轴交于A、B两点,与y轴交于点C(0. ).且对称抽x=l.
).且对称抽x=l.
(1)求出抛物线的解析式及A、B两点的坐标;
(2)在x轴下方的抛物线上是否存在点D,使四边形ABDC的面积为3.若存在,求出点D的坐标;若不存在.说明理由(使用图1);
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,请求出所有满足条件的点P的坐标(使用图2).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏无锡宜兴市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,抛物线 与x轴交于A、C两点,与y轴交于B点.
与x轴交于A、C两点,与y轴交于B点.

(1)求△AOB的外接圆的面积;
(2)若动点P从点A出发,以每秒1个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒0.5个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动.问当t为何值时,以A、P、Q为顶点的三角形与△OAB相似?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
问:是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com