
 )、B(2,-4)是一次函数
)、B(2,-4)是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点。
的图象的两个交点。 轴的交点C的坐标及△AOB的面积;
轴的交点C的坐标及△AOB的面积; 的解(请直接写出答案);
的解(请直接写出答案); 的解集(请直接写出答案)。
的解集(请直接写出答案)。
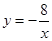 , y="-x-2;" (2) C(-2,0),6.(3)x1=-4,x2=2.(4)-4<x<0或x>2.
, y="-x-2;" (2) C(-2,0),6.(3)x1=-4,x2=2.(4)-4<x<0或x>2. 的图象的两个交点,利用待定系数法即可求得反比例函数和一次函数的解析式;
的图象的两个交点,利用待定系数法即可求得反比例函数和一次函数的解析式; 的解即是求函数y=kx+b以函数
的解即是求函数y=kx+b以函数 的交点的横坐标.
的交点的横坐标. 的解集.
的解集. 的图象上,
的图象上,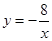 .
.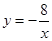 的图象上,
的图象上, ,解之得:
,解之得: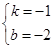 .
.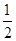 OC•n+
OC•n+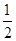 OC×4=
OC×4=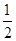 ×2×2+
×2×2+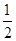 ×2×4=6.
×2×4=6.

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 恒过定点
恒过定点 .
. 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标; ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.12 | B.-6 | C.6或12 | D.-6或-12 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
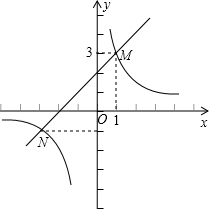
 与直线
与直线 交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程
交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程 的解为
的解为| A.-3,1 | B.-3,3 | C.-1,1 | D.-1,3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
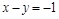 的解为坐标的点在平面直角坐标系中的图象是一条直线。根据这个结论,在同一平面直角坐标系中画出二元一次方程组
的解为坐标的点在平面直角坐标系中的图象是一条直线。根据这个结论,在同一平面直角坐标系中画出二元一次方程组 中两个二元一次方程的图象,并根据图象写出这个二元一次方程组的解。
中两个二元一次方程的图象,并根据图象写出这个二元一次方程组的解。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 随着所处深度
随着所处深度 的变化而变化,在某个地点
的变化而变化,在某个地点 与
与 的关系可以由公式
的关系可以由公式 来表示,则
来表示,则 随
随 的增大1而( )
的增大1而( )| A.增大35 | B.减小 35 | C.不变 | D.以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com