
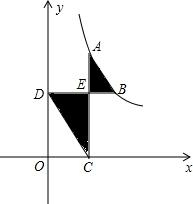
 如图,AB=
如图,AB= ,线段AB的两端点在函数y=
,线段AB的两端点在函数y=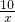 (x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于________.
(x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于________.
 -2a,BE=
-2a,BE=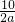 -a,再利用勾股定理求出a的值,进而得出阴影部分的面积.
-a,再利用勾股定理求出a的值,进而得出阴影部分的面积. ),B(
),B(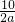 ,2a),
,2a), -2a,BE=
-2a,BE=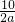 -a,
-a, ,
, -2a)2+(
-2a)2+(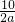 -a)2=(
-a)2=( )2,
)2,
 或a2=4,
或a2=4, ×DE×EC+
×DE×EC+ AE×BE=
AE×BE= ×2×4+
×2×4+ ×1×0.5=4
×1×0.5=4 .
. .
. 的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.
的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键. 

科目:初中数学 来源:2013年湖南省邵阳市中考数学模拟试卷(二)(解析版) 题型:填空题
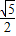 ,线段AB的两端点在函数y=
,线段AB的两端点在函数y=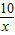 (x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于 .
(x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于 .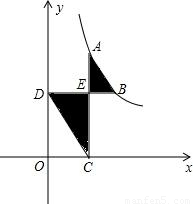
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com