
��12�֣���ͼ������ABCD�У�AD��BC��BC��20cm��AD��10cm��������������P��Q
�ֱ��B��D����ͬʱ��������P��ÿ��2cm���ٶ���BC���յ�C�ƶ�����Q��ÿ��1cm
���ٶ���DA���յ�A�ƶ����߶�PQ��BD�ཻ�ڵ�E����E��EF��BC��CD�ڵ�F������
QF��BC���ӳ����ڵ�H���趯��P��Q�ƶ���ʱ��Ϊt����λ���룬0<t<10����
��1����tΪ��ֵʱ���ı���PCDQΪƽ���ı��Σ�
��2����P��Q�ƶ��Ĺ����У��߶�PH�ij��Ƿ����ı䣿������䣬����߶�PH�ij�������ı䣬��˵�����ɣ�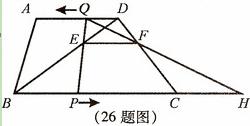
 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪����ͼ������ABCD�У�AD��BC����B=45�㣬��C=120�㣬AB=8����CD�ij�Ϊ��������
��֪����ͼ������ABCD�У�AD��BC����B=45�㣬��C=120�㣬AB=8����CD�ij�Ϊ��������A��
| ||||
B��4
| ||||
C��
| ||||
D��4
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 5����֪����ͼ������ABCD�У�AD��BC��AB=DC��AC��BD�ཻ�ڵ�O����ô��ͼ��ȫ�������ι���
5����֪����ͼ������ABCD�У�AD��BC��AB=DC��AC��BD�ཻ�ڵ�O����ô��ͼ��ȫ�������ι����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 10����ͼ������ABCD�У�AD��BC��BDΪ�Խ��ߣ���λ��EF��BD��O�㣬��FO-EO=3����BC-AD���ڣ�������
10����ͼ������ABCD�У�AD��BC��BDΪ�Խ��ߣ���λ��EF��BD��O�㣬��FO-EO=3����BC-AD���ڣ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ������ABCD�У���֪AD��BC����A=90�㣬AB=7��AD=2��cosC=
��ͼ������ABCD�У���֪AD��BC����A=90�㣬AB=7��AD=2��cosC=
| ||
| 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ������ABCD�У�AD��BC��BC=5��AD=3���Խ���AC��BD���ҡ�DBC=30�㣬������ABCD�ĸߣ�
��ͼ������ABCD�У�AD��BC��BC=5��AD=3���Խ���AC��BD���ҡ�DBC=30�㣬������ABCD�ĸߣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com