
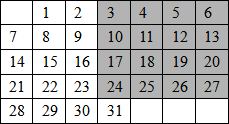
 如图是一张某月份的日历:
如图是一张某月份的日历:| 25 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图是2013年某月份的月历:
星期 一 二 三 四 五 六 日
1
![]() 2 3 4 5 6 7 8
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
![]() 23 24 25 26 27 28 29
23 24 25 26 27 28 29
30 31
⑴用一个平行四边形在这张月历中任意框出四个数,设左上角第一个数为x,那么右下角的数为____________,这四个数和为_______________(用x的代数式表示) .
⑵用上题的方法在这张月历中框出的四个数之和是否可能等于102?若有可能,请求出这四个数分别是几号;若不可能,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com