
(本小题满分12分)点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A,B两点(点A在点B的上方),点Q为点P旋转后的对应点.
(1)当m=2,点P横坐标为4时,求Q点的坐标;
(2)设点Q(a,b),用含m,b的代数式表示a;(直接写出结果)
(3)如图,点Q在第一象限内,点D在并轴的正半轴上,点C为OD的中点,QD平分∠AQC,AQ=2QC,当QD=m时,求m的值.

(1)Q(-2,2)(2)a=m-b2.(3)m=1.
【解析】
试题分析:(1) 连接QG,PG,过点Q作QF⊥x轴于点,,过点P作PE⊥x轴于点E,要想求Q点的坐标,只需要求出FO,FQ的长即可,而证明ΔCQF≌ΔPGE可得;(2) 用含m,b的代数式表示a,a=m-b2.(3) 延长QC到点E,使CE=CQ,连接OE,然后可证ΔECO≌ΔQCD,ΔAQO≌ΔEQO,从而可得OE=DQ=m,AO=EO=m,根据A(0,m)在新的图象上,可得0=m-m2,解得m1=1,m2=0(舍).所以m=1.
试题解析:【解析】
(1)当m=2时,y=(x-2)2,则G(2,0),P(4,4).(1分)
如图,连接QG,PG,过点Q作QF⊥x轴于点,,过点P作PE⊥x轴于点E.
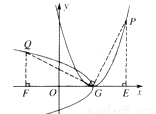
依题意,可得ΔCQF≌ΔPGE, (3分)
则FQ=EG=2,FG=EP=4,
∴FO=2,∴Q(-2,2). (5分)
(2)用含m,b的代数式表示a,a=m-b2. (8分)
(3)如图,延长QC到点E,使CE=CQ,连接OE.
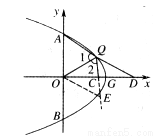
∵C为OD中点,∴OC=CD.
∵∠ECO=∠QCD,∴ΔECO≌ΔQCD.
∴OE=DQ=m. (9分)
∵AQ=2QC,∴AQ=QE.
∵QO平分∠AQC,∴∠1=∠2.
∴ΔAQO≌ΔEQO. (10分)
∴AO=EO=m.∴A(0,m). (11分)
∵A(0,m)在新的图象上,∴0=m-m2.
∴m1=1,m2=0(舍).∴m=1. (12分)
考点:1.函数与坐标轴的交点;2.全等三角形的判定与性质;3.一元二次方程.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源:2014-2015学年浙江省宁波市宁海县东片九年级上学期第三次月考数学试卷(解析版) 题型:选择题
小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图所示,为配到一块与原来 大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
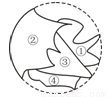
A.第①块 B.第②块 C.第③块 D.第④块
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,把一块含有45°角的直角三角板两个顶点放在直尺的对边上,如果∠1=20°,则∠2的度数是( )
A.15° B.20° C.25° D.30°

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期学业水平模拟数学试卷(解析版) 题型:选择题
已知二次函数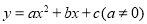 的图象如图所示,则直线
的图象如图所示,则直线 与反比例函数
与反比例函数 ,在同一坐标系内的大致图象为( )
,在同一坐标系内的大致图象为( )

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期学业水平模拟数学试卷(解析版) 题型:选择题
一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为( )

A.6个 B.8个 C.12个 D.17个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级下学期学业水平模拟考试1数学试卷(解析版) 题型:解答题
(本小题满分l0分)如图所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为140cm.现已测量出屋顶斜面与水平面夹角为θ2,并已知tanθ1≈1.1,tanθ2≈0.4.如果安装工人已确定支架加高为25 cm,求支架CD的高(结果精确到1 cm)?
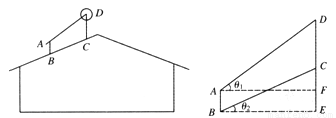
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级下学期学业水平模拟考试1数学试卷(解析版) 题型:填空题
若一个直角三角形的两直角边上的中线长分别是3和4,则该直角三角形的斜边长是_____.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:解答题
如图,小山岗的斜坡AC的坡度是tanα=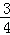 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
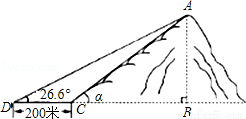
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com