
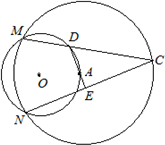
 已知:如图,⊙O与⊙A交于M、N点,且点A在⊙O上,弦MC交⊙O于D点,连接AD、NC,并延长DA交NC于E.
已知:如图,⊙O与⊙A交于M、N点,且点A在⊙O上,弦MC交⊙O于D点,连接AD、NC,并延长DA交NC于E.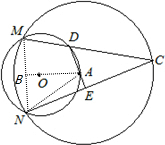


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
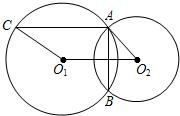
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.查看答案和解析>>
科目:初中数学 来源: 题型:
 ,⊙O2的半径为
,⊙O2的半径为| 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com