
在平面直角坐标系中,抛物线y=ax2+bx+2的图象过 和
和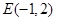 ,与
,与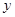 轴交于点
轴交于点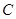 ,与
,与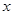 轴交于另一点
轴交于另一点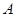 ,点
,点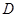 是原点
是原点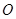 关于点
关于点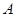 的对称点,连结
的对称点,连结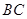 、
、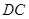 ,设点
,设点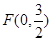 。
。
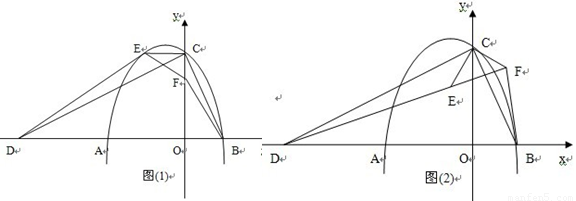
(1)求抛物线的解析式;
(2)连结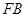 、
、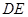 ,①求
,①求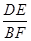 的值;②将
的值;②将 绕点
绕点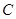 旋转,在旋转过程中如图(2),线段
旋转,在旋转过程中如图(2),线段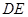 和
和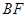 的比值会变吗?请说明理由;
的比值会变吗?请说明理由;
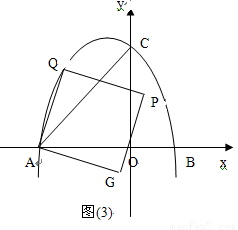
(3)设点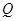 是直线
是直线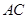 上方的抛物线上一点,连结
上方的抛物线上一点,连结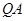 ,以
,以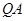 为边作图示一侧的正方形,随着点
为边作图示一侧的正方形,随着点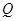 的运动,正方形的大小,位置也随之改变,当顶点
的运动,正方形的大小,位置也随之改变,当顶点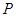 或
或 恰好落在
恰好落在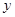 轴上时,直接写出对应点
轴上时,直接写出对应点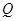 的坐标。
的坐标。
(1)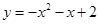 (2)①2②不变,理由见解析(3)
(2)①2②不变,理由见解析(3) ,
,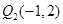 ,
,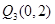
【解析】解:(1)∵图象经过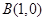 、
、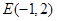 ,代入
,代入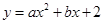
得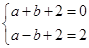 解得
解得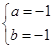 ∴
∴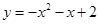
(2)①设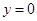 ,则
,则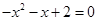
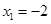 ,
,
∴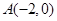 ∴
∴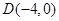
作EM⊥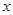 轴,
轴,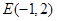 ∴MO=1
∴MO=1
∴AM=1 ∴DM=2+1=3
EM=2 ∴DE=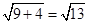 BF=
BF=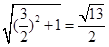
∴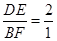
②成立。∵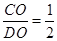 ,
,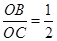 ∴
∴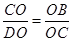 ,∠COB=∠DOC=Rt∠
,∠COB=∠DOC=Rt∠
∴△COB∽△DOC ∴∠BCO=∠CDO
又∵∠CDO+∠DCO=90° ∴∠BCO+∠DCO=90°
∴∠DCB=90° ∴∠DCE+∠ECB=∠CFD+∠BCE==90°
∴∠DCE =∠CFD
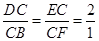
∴△DEC∽△BCF
∴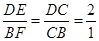
③当H点在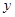 轴上时,如图,作QH⊥
轴上时,如图,作QH⊥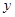 轴于H
轴于H
QN⊥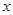 轴于N ∵QP=QA ∠AQN=∠PQN ∠QNA+∠QHP=90°
轴于N ∵QP=QA ∠AQN=∠PQN ∠QNA+∠QHP=90°
∴△QAN≌△QPH ∴QH=QN即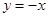
∴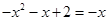 ∴
∴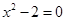 ∴
∴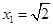 (舍去),
(舍去),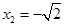
∴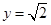 ∴
∴
当G在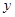 轴上时,则△QAN≌△AOG
轴上时,则△QAN≌△AOG
∴QN=AO=2即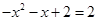
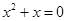
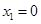 ,
,
∴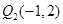 ,
,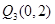
(1)用待定系数法求得
(2)①设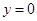 ,求得A、D点的坐标,作EM⊥
,求得A、D点的坐标,作EM⊥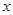 轴,根据勾股定理求得DE、 BF 的长,从而求得
轴,根据勾股定理求得DE、 BF 的长,从而求得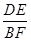 的值;②通过证得△COB∽△DOC,再证得△DEC∽△BCF,即可得出结论
的值;②通过证得△COB∽△DOC,再证得△DEC∽△BCF,即可得出结论
(3)分两种情况进行讨论: 当H点在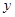 轴上时, 当G在
轴上时, 当G在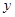 轴上时
轴上时


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com