
| CE |
| CD |
| 1 |
| 2 |
| AM |
| BN |
| CE |
| CD |
| 1 |
| 3 |
| AM |
| BN |
| CE |
| CD |
| 1 |
| 4 |
| AM |
| BN |
| CE |
| CD |
| 1 |
| n |
| AM |
| BN |
| AB |
| BC |
| 1 |
| m |
| CE |
| CD |
| 1 |
| n |
| AM |
| BN |
| CE |
| CD |
| 1 |
| 2 |
| AM |
| BN |
| 1 |
| 5 |
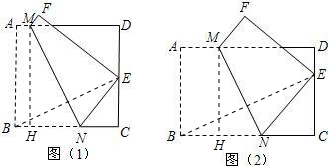
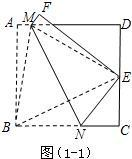 解:(1)方法一:如图(1-1),连接BM,EM,BE.
解:(1)方法一:如图(1-1),连接BM,EM,BE.| CE |
| CD |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| AM |
| BN |
| 1 |
| 5 |
| 5 |
| 4 |
| 5 |
| 4 |
|
| 5 |
| 4 |
| 1 |
| 4 |
| AM |
| BN |
| 1 |
| 5 |
| CE |
| CD |
| 1 |
| n |
| n2+1 |
| 2n |
| n2+1 |
| 2n |
| n2-2n+1 |
| 2n |
| AM |
| BN |
| ||
|
| n2-2n+1 |
| n2+1 |
| CE |
| CD |
| 1 |
| 3 |
| AM |
| BN |
| 2 |
| 5 |
| CE |
| CD |
| 1 |
| 4 |
| AM |
| BN |
| 9 |
| 17 |
| CE |
| CD |
| 1 |
| n |
| AB |
| BC |
| 1 |
| m |
| n |
| mn |
| m2n2+1 |
| 2mn |
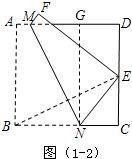
| MH |
| BC |
| HN |
| CE |
| n |
| mn |
| HN |
| 1 |
| 1 |
| m |
| m2n2-2n+1 |
| 2mn |
| AM |
| BN |
| ||
|
| m2n2-2n+1 |
| m2n2+1 |
| 1 |
| 5 |
| 9 |
| 17 |
| (n-1)2 |
| n2+1 |
| n2m2-2n+1 |
| n2m2+1 |


科目:初中数学 来源: 题型:阅读理解
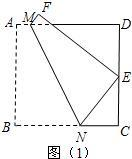
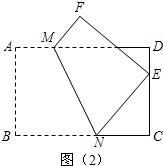
 25、阅读下面问题的解决过程:
25、阅读下面问题的解决过程:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 问题解决:如图是一块长方形ABCD的运动场地,长AD=101m,宽AB=52m,从B,C两处入口的两条小路宽度相等,两条小路汇合处的路宽为B,C处入口宽的2倍,其余部分种植草坪,若草坪面积为5049m2,求B、C处入口小路的宽.
问题解决:如图是一块长方形ABCD的运动场地,长AD=101m,宽AB=52m,从B,C两处入口的两条小路宽度相等,两条小路汇合处的路宽为B,C处入口宽的2倍,其余部分种植草坪,若草坪面积为5049m2,求B、C处入口小路的宽.查看答案和解析>>
科目:初中数学 来源: 题型:
 问题解决.
问题解决.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com