
如图,已知经过原点的抛物线y=-2x2+4x与x轴的另一交点为A,现将它向右平移M(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P.
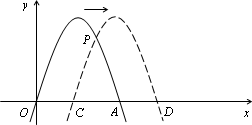
(1)求点A的坐标,并判断△PCA存在时它的形状(不要求说理);
(2)在x轴上是否存在两条相等的线段?若存在,请一一找出,并写出它们的长度(可用含m的式子表示);若不存在,请说明理由;
(3)设△PCD的面积为S,求S关于m的关系式.
|
解:(1)令-2x2+4x=0,得x1=0,x2=2 ∴点A的坐标为(2,0) 2分 △PCA是等腰三角形 3分 (2)存在OC=AD=m,OA=CD=2 5分 (3)当0<m<2时,如下图,作PH⊥x轴于H,设P(xp,yp)
∵A(2,0),C(m,0), ∴AC=2-m ∴ ∴ 把 ∵CD=OA=2, ∴ 当m=2时,△PCD不存在 当m>2时,如下图,作PH⊥x轴于H,设P(xp,yp)
∵A(2,0),C(m,0), ∴AC=m-2,∴AH= ∴ 把 得 ∵CD=OA=2, ∴ 说明:采用 |


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
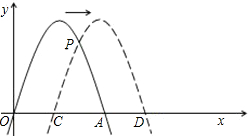 们的长度(可用含m的式子表示);若不存在,请说明理由;
们的长度(可用含m的式子表示);若不存在,请说明理由;查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(31):34.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市密云县九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(32):2.8 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(28):20.5 二次函数的一些应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com