
 小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.分析 (1)根据两直线平行,内错角相等可得结论;
(2)根据同圆的半径相等得:PD=PA,由等边对等角得:∠PDA=∠PAB,由平行线的性质和对顶角相等可得:∠GBA=∠PDA=∠BDC=∠PAB.
解答 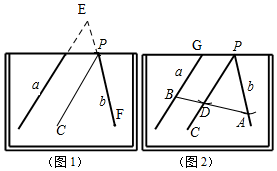 解:(1)如图1,作出直线a、b所成的角E,
解:(1)如图1,作出直线a、b所成的角E,
∵PC∥a,
∴∠E=∠CPF,
即直线b与PC的夹角度数,即直线a,b所成角的度数.
(2)如图2,∠GBA=∠PDA=∠BDC=∠PAB,理由是:
∵PD=PA,
∴∠PDA=∠PAB,
∵PC∥a,
∴∠GBA=∠PDA,
∴∠GBA=∠PDA=∠PAB,
∵∠BDC=∠PDA,
∴∠GBA=∠PDA=∠BDC=∠PAB.
点评 本题考查了平行线的性质和作图问题,熟练掌握平行线的性质是关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
| 行驶时间(时) | 1 | 2 | 3 | 4 | 5 |
| 余油量(升) | 55 | 50 | 45 | 40 | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线a、b交于O点,夹角为45°,A、B分别为直线a,b上异于O的点,P为同一平面内不在直线a,b上的定点,且P、A、B不共线,求当△PAB的周长为最小值时,∠APB的度数.
如图,直线a、b交于O点,夹角为45°,A、B分别为直线a,b上异于O的点,P为同一平面内不在直线a,b上的定点,且P、A、B不共线,求当△PAB的周长为最小值时,∠APB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
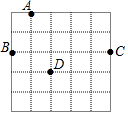 如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )
如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com