
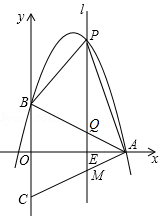
 ��ͼ���ڵ���������ABC�У�AB=AC���Եױ�BC�Ĵ�ֱƽ���ߺ�BC���ڵ�ֱ�߽���ƽ��ֱ������ϵ�������� y=-$\frac{1}{2}$x2+$\frac{7}{2}$x+4����A��B���㣮
��ͼ���ڵ���������ABC�У�AB=AC���Եױ�BC�Ĵ�ֱƽ���ߺ�BC���ڵ�ֱ�߽���ƽ��ֱ������ϵ�������� y=-$\frac{1}{2}$x2+$\frac{7}{2}$x+4����A��B���㣮���� ��1���ֱ�x=0��y=0�������õ�A��B�����ꣻ
��2������ֱ��AB�Ľ���ʽ����ʾ��P��Q�����꼰PQ�ij������ݡ�ABP�����=Ǧֱ�߶�PQ��ˮƽ����OA�������������S��t�ĺ�����ϵʽ���䷽��������������
��3�����ݣ�2������õĽ���ʽ����S��APB=$\frac{3}{4}$S��ABC�����x��ֵ����������������ö�Ӧ��yֵ����ó���P�����꣮
��� �⣺��1����x=0ʱ��y=4��
��B��0��4����
��y=0ʱ��-$\frac{1}{2}$x2+$\frac{7}{2}$x+4=0��
��ã�x=8��-1��
��A��8��0����
��2����AB�Ľ���ʽΪ��y=kx+b��
��A��8��0����B��0��4������ã�$\left\{\begin{array}{l}{8k+b=0}\\{b=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$��
��AB�Ľ���ʽΪ��y=-$\frac{1}{2}$x+4��
��Q��t��-$\frac{1}{2}$t+4����P��t��-$\frac{1}{2}$t2+$\frac{7}{2}$t+4����
��PQ=��-$\frac{1}{2}$t2+$\frac{7}{2}$t+4��-��-$\frac{1}{2}$t+4��=-$\frac{1}{2}$t2+4t��
��S=$\frac{1}{2}$PQ•OA=$\frac{1}{2}$��-$\frac{1}{2}$t2+4t����8=-2t2+16t=-2��t-4��2+32��
��0��t��8��
�൱t=4ʱ��S�����ֵΪ32��
����ABP��������Ϊ32��
��3�����ڣ�
��OA��BC�Ĵ�ֱƽ���ߣ�
��OB=OC=4��
��OA=8��
��S��ABC=$\frac{1}{2}$BC•OA=$\frac{1}{2}$��8��8=32��
��S��APB=$\frac{3}{4}$S��ABC��
��-2t2+16t=$\frac{3}{4}��32$��
t2-8t=-12��
t2-8t+12=0��
��t-2����t-6��=0��
��ã�t=2��6��
��t=2ʱ��y=-$\frac{1}{2}$��22+$\frac{7}{2}$��2+4=9��
��t=6ʱ��y=-$\frac{1}{2}$��62+$\frac{7}{2}$��6+4=7��
���P��������2��9����6��7����
���� �����Ƕ��κ������ۺ��⣬�Ѷ����У�����������������������Ľ���Ͷ��κ�������ֵ���⣬��ȷ���κ�������ֵ���䷶Χ���Ƕ������꣬���������ε������������Ǧֱ�߶Ⱥ�ˮƽ���ȵij˻�����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��-3 | B�� | m��-3��m��6 | C�� | m��-3��m��6 | D�� | m��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
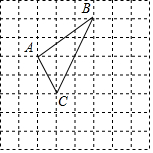 ��ͼ����8��8�������������У�ÿ��С�����εı߳���Ϊ1���С�ABC����A��B��C����С�����εĶ����ϣ�
��ͼ����8��8�������������У�ÿ��С�����εı߳���Ϊ1���С�ABC����A��B��C����С�����εĶ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
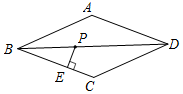 ��ͼ��P������ABCD�Խ���BD�ϵ�һ�㣬PE��BC�ڵ�E��PE=4cm�����P��ֱ��AB�ľ������4cm��
��ͼ��P������ABCD�Խ���BD�ϵ�һ�㣬PE��BC�ڵ�E��PE=4cm�����P��ֱ��AB�ľ������4cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
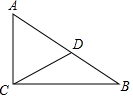 ��ͼ����֪Rt��ABC�У���ACB=90�㣬D��AB���е㣬CD=3cm����AB=6cm��
��ͼ����֪Rt��ABC�У���ACB=90�㣬D��AB���е㣬CD=3cm����AB=6cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
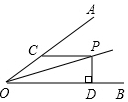 ��ͼ��OPƽ�֡�AOB����AOP=15�㣬PC��OB��PD��OB�ڵ�D��PD=4����PC����8��
��ͼ��OPƽ�֡�AOB����AOP=15�㣬PC��OB��PD��OB�ڵ�D��PD=4����PC����8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
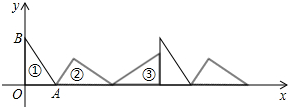
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com