
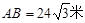 ,
,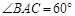 .设
.设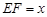 米,
米,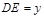 米.
米.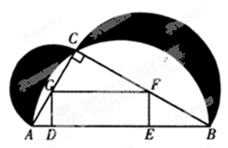
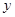 与
与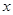 之间的函数解析式;
之间的函数解析式;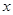 为何值时,矩形的面积最大?最大面积是多少?
为何值时,矩形的面积最大?最大面积是多少?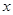 为何值时,矩形的面积等于两弯新月面积的
为何值时,矩形的面积等于两弯新月面积的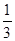 ?
? ﹣
﹣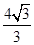 x(0<x<18);
x(0<x<18); 平方米;
平方米; )米时,矩形DEFG的面积及等于两弯新月面积的
)米时,矩形DEFG的面积及等于两弯新月面积的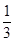 .
. 米,BC=36米,∠ABC=30°,再根据三角函数的定义求出AD=
米,BC=36米,∠ABC=30°,再根据三角函数的定义求出AD=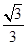 x,BE=
x,BE= x,然后根据AD+DE+BE=AB,列出y与x之间的关系式,进而求解即可;
x,然后根据AD+DE+BE=AB,列出y与x之间的关系式,进而求解即可; ﹣
﹣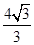 x代入,得出矩形DEFG的面积=xy=﹣
x代入,得出矩形DEFG的面积=xy=﹣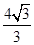 x2+24
x2+24 x,然后利用配方法写成顶点式,根据二次函数的性质即可求解;
x,然后利用配方法写成顶点式,根据二次函数的性质即可求解;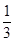 列出关于x的一元二次方程,解方程即可求解.
列出关于x的一元二次方程,解方程即可求解. 米,∠BAC=60°,
米,∠BAC=60°,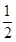 AB=12
AB=12 米,BC=
米,BC= AC=36米,∠ABC=30°,
AC=36米,∠ABC=30°,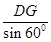 =
=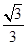 x,BE=
x,BE=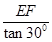 =
= x,
x,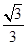 x+y+
x+y+ x=24
x=24 ,
, ﹣
﹣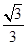 x﹣
x﹣ x=24
x=24 ﹣
﹣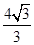 x,
x, ﹣
﹣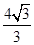 x(0<x<18);
x(0<x<18); ﹣
﹣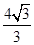 x,
x, ﹣
﹣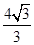 x)=﹣
x)=﹣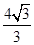 x2+24
x2+24 x=﹣
x=﹣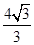 (x﹣9)2+108
(x﹣9)2+108 ,
, 平方米;
平方米; πAC2,S2=
πAC2,S2= πBC2,S3=
πBC2,S3= πAB2,
πAB2,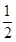 AC•BC=
AC•BC=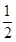 ×12
×12 ×36=216
×36=216 (平方米).
(平方米).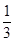 ,
,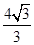 (x﹣9)2+108
(x﹣9)2+108 =
=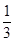 ×216
×216 ,
, ,符合题意.
,符合题意. )米时,矩形DEFG的面积及等于两弯新月面积的
)米时,矩形DEFG的面积及等于两弯新月面积的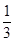 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
 的图像经过点
的图像经过点 和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,试用
,试用 表示
表示 (直接写出答案)
(直接写出答案)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
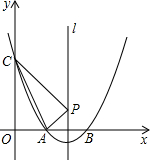
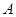 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与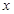 轴相交于点
轴相交于点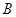 ,连结
,连结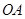 ,抛物线y=x
,抛物线y=x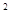
 从点
从点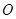 沿
沿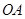 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点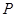 ,顶点
,顶点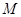 到
到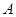 点时停止移动.
点时停止移动.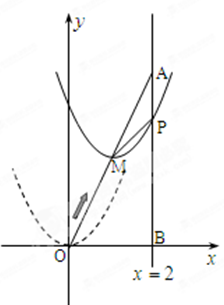
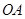 所在直线的函数解析式;
所在直线的函数解析式;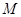 的横坐标为
的横坐标为 ,
, 的代数式表示点
的代数式表示点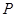 的坐标;
的坐标; 为何值时,线段
为何值时,线段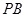 最短;
最短;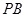 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△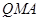 的面积与△
的面积与△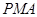 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
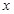 与函数值
与函数值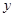 的对应值,判断方程ax2+b x+c=0(a≠0)的一个解
的对应值,判断方程ax2+b x+c=0(a≠0)的一个解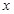 的范围是( )
的范围是( ) 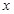 | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 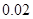 |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com