
分析 (1)根据b是最小的正整数即可确定b=1,然后根据非负数的性质确定c和a的值;
(2)对x的范围分成0≤x≤1和1<x≤2两种情况,根据绝对值的性质去掉绝对值符号,然后加减即可.
解答 解:(1)∵b是最小的正整数,
∴b=1.
根据题意得:c-5=0,a+b=0,
∴a=-1,b=1,c=5;
(2)当0≤x≤1时,x+1>0,x-1≤0,x+3>0,
则:|x+1|-|x-1|+2|x+3|
=x+1-(1-x)+2(x+3)
=x+1-1+x+2x+6
=4x+6;
当1<x≤2时,x+1>0,x-1>0,x+3>0.
∴|x+1|-|x-1|+2|x+3|=x+1-(x-1)+2(x+3)
=x+1-x+1+2x+6
=2x+8.
点评 本题考查了非负数的性质以及绝对值的性质,正确对x进行分类讨论是关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
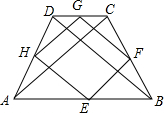 四边形ABCD中,DC∥AB,AC⊥BD,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.
四边形ABCD中,DC∥AB,AC⊥BD,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com