
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
甲乙二人练习跑步.如果甲让乙先跑10米,甲跑5秒钟就追上乙; 如果先让乙跑2秒钟,那么甲跑4秒钟就追上乙.若设甲,乙每秒钟分别跑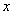 米,
米, 米, 列方程组是( )
米, 列方程组是( )
(A)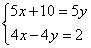 (B)
(B)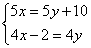
(C)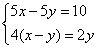
 (D)
(D)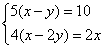
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的口袋中装有红球6个,黄球9个,绿球3个,这些球除了颜色外,没有其它任何区别。现在从中任意摸出一个球,
(1)计算摸到的绿球的概率;
(2)如果要使摸到的绿球的概率是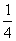 ,需要在这个口袋中拿走多少个其他颜色的球?
,需要在这个口袋中拿走多少个其他颜色的球?
(3)在(2)中,除了拿走其它颜色的球,你还有什么方法使摸到的绿球的概率仍为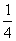 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢? 如图甲,∠FDC、∠ECD为△ADC的两个外角,则∠A与∠FDC+∠ECD的数量关系 . |




探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有 何种关系?
何种关系?
如图乙,在△ADC中,DP、CP分别平分∠ADC和∠ACD,则∠P与∠A的数量关系 .
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图丙,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,则∠P与∠A+∠B的数量关系 .
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?如图丁
则∠P与∠A+∠B+∠E+∠F的数量关系 .
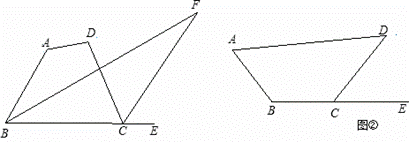
探究五:如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β;
(1)如图①,α+β>180°,则∠F= ;(用α,β表示)
(2)如图②,α+β< 180°,请在图中画出∠F,且∠F= ;(用α,β表示)
180°,请在图中画出∠F,且∠F= ;(用α,β表示)
(3 )一定存在∠F吗?如有,直接写出∠F的值,如不一定,直接指出α,β满足什么条件时,不存在∠F.
)一定存在∠F吗?如有,直接写出∠F的值,如不一定,直接指出α,β满足什么条件时,不存在∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题错误的是( )
A.有一组邻边相等的平行四边形叫做正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
D.有一个角是直角的菱形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com