
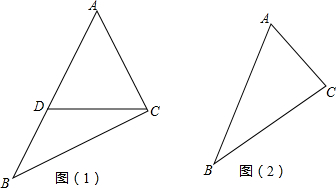
分析 (1)①如图1,利用三角形外角性质得∠ADC=∠B+∠BCD,加上∠ACD=∠ACB-∠BCD,∠ADC=∠ACD,于是∠B+∠BCD=∠ACB-∠BCD,易得∠BCD=$\frac{1}{2}$(α-β),然后把α=90°,β=36°代入计算可得到∠BCD的度数;
②由①可得∠BCD与α和β的关系;
(2)如图2,利用三角形内角和得到∠ADC=180°-∠B-∠BCD,加上∠ACD=∠BCD-∠ACB,∠ADC=∠ACD,则180°-∠B-∠BCD=∠BCD-∠ACB,然后整理即可得到∠BCD与α和β的关系.
解答 解:(1)①如图1,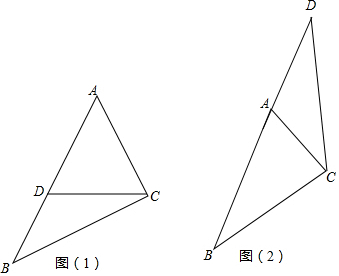
∵∠ADC=∠B+∠BCD,∠ACD=∠ACB-∠BCD,
而∠ADC=∠ACD,
∴∠B+∠BCD=∠ACB-∠BCD,
即β+∠BCD=α-∠BCD,
∴∠BCD=$\frac{1}{2}$(α-β),
当α=90°,β=36°,∠BCD=$\frac{1}{2}$(90°-36°)=27°;
故答案为27;
②由①得∠BCD=$\frac{1}{2}$(α-β),
(2)如图2,∵∠ADC=180°-∠B-∠BCD,∠ACD=∠BCD-∠ACB,
而∠ADC=∠ACD,
∴180°-∠B-∠BCD=∠BCD-∠ACB,
即180°-β-∠BCD=∠BCD-α,
∴∠BCD=90°-$\frac{1}{2}$(α-β).
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.


科目:初中数学 来源: 题型:解答题
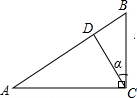 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=10,AC=8.求:
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=10,AC=8.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com