A
分析:要求CE的长,应先设CE的长为x,由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AFE,所以AF=10cm,EF=DE=(8-x)cm;在Rt△ABF中由勾股定理得:AB
2+BF
2=AF
2,已知AB、AF的长可求出BF的长,又CF=BC-BF=10-BF,在Rt△ECF中由勾股定理可得:EF
2=CE
2+CF
2,即:(8-x)
2=x
2+(10-BF)
2,将求出的BF的值代入该方程求出x的值,即求出了CE的长.
解答:根据折叠方式可得:△AED≌△AEF,
∴AF=AD=BC=10cm,DE=EF,
设EC=xcm,则DE=(8-x)cm.
∴EF=(8-x)cm,
在Rt△ABF中,BF=

=6cm,
∴FC=BC-BF=4cm.
在Rt△CEF中,由勾股定理得:CE
2+FC
2=EF
2,
即:x
2+4
2=(8-x)
2,
解得x=3.
∴EC的长为3cm.
故选:A.
点评:本题主要考查了勾股定理,折叠问题的应用;两次利用勾股定理得到所需线段长是解决本题的关键.

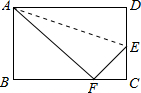 已知如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则EC=
已知如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则EC= =6cm,
=6cm,
