
 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | $\frac{π}{6}$ | C. | 4$\sqrt{3}$-$\frac{2π}{3}$ | D. | 2$\sqrt{3}$-$\frac{2π}{3}$ |
分析 首先求出∠AOB,OB,然后利用S阴=S△ABO-S扇形OBD计算即可.
解答 解:连接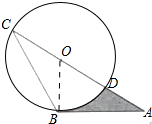 OB.
OB.
∵AB是⊙O切线,
∴OB⊥AB,
∵OC=OB,∠ABC=30°,
∴∠C=∠OBC=30°,
∴∠AOB=∠C+∠OBC=60°,
在Rt△ABO中,∵∠ABO=90°,AB=2$\sqrt{3}$,∠A=30°,
∴OB=2,
∴S阴=S△ABO-S扇形OBD=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60•π•{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$.
故选D.
点评 本题考查切线的性质、等腰三角形的性质、勾股定理,直角三角形30度角性质,解题的关键是学会分割法求面积,记住扇形面积公式,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
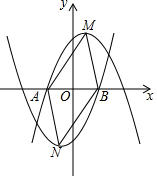 如图,在平面直角坐标系中,抛物线y=-(x-h)2+2(h>0)的顶点为M,与x轴负半轴的交点为A,抛物线y=(x+h)2-2的顶点为N,与x轴正半轴的交点为B,若AB=2h,则四边形MANB的面积为2$\sqrt{2}$.
如图,在平面直角坐标系中,抛物线y=-(x-h)2+2(h>0)的顶点为M,与x轴负半轴的交点为A,抛物线y=(x+h)2-2的顶点为N,与x轴正半轴的交点为B,若AB=2h,则四边形MANB的面积为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
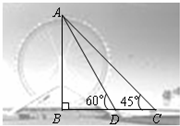 2016年,合肥万达主题乐园开门迎客,合肥万达全国诸多万达乐园中惟一拥有摩天轮的项目,亦是园区内天际线的重要组成部分,是园区内观赏风光的最佳选择.某校数学兴趣小组要测量摩天轮的高度,如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°,求该兴趣小组测得的摩天轮的高度AB.
2016年,合肥万达主题乐园开门迎客,合肥万达全国诸多万达乐园中惟一拥有摩天轮的项目,亦是园区内天际线的重要组成部分,是园区内观赏风光的最佳选择.某校数学兴趣小组要测量摩天轮的高度,如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°,求该兴趣小组测得的摩天轮的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图:
老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
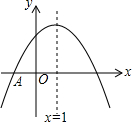 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
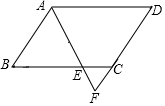 如图,在?ABCD中,AB=6,AD=9,∠BAD=120°且∠BAD的平分线交BC于点E,交DC的延长线于点F,则△CEF的周长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD=120°且∠BAD的平分线交BC于点E,交DC的延长线于点F,则△CEF的周长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com