
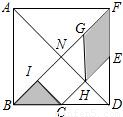
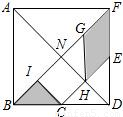
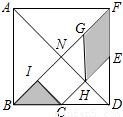
 解:(1)由七巧板性质可知,BI=IC=CH=HE.(字母I就是字母P)
解:(1)由七巧板性质可知,BI=IC=CH=HE.(字母I就是字母P) BI•IC=1,
BI•IC=1,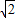 ,
,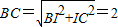 .
.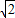

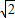 ,
,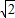 sin45°,
sin45°,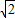 sin45°
sin45° ×
×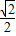 =2.
=2.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《反比例函数》(02)(解析版) 题型:选择题
 (k≠0)的图象上任一点,过P点分别作x轴,y轴的平行线,若两平行线与坐标轴围成矩形的面积为2,则k的值为( )
(k≠0)的图象上任一点,过P点分别作x轴,y轴的平行线,若两平行线与坐标轴围成矩形的面积为2,则k的值为( )查看答案和解析>>
科目:初中数学 来源:2006年广东省茂名市中考数学试卷(解析版) 题型:解答题
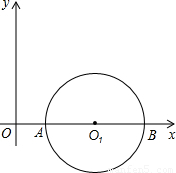
查看答案和解析>>
科目:初中数学 来源:2006年广东省茂名市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com