
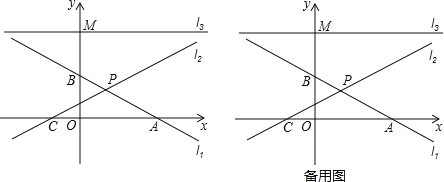
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��l1��y=��![]() x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��ֱ��l2��y=kx+2k��x�ύ�ڵ�C����ֱ��l1���ڵ�P��
x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��ֱ��l2��y=kx+2k��x�ύ�ڵ�C����ֱ��l1���ڵ�P��
��1��ֱ��l2�Ƿ�x����һ���㣿����������ֱ��д���������ꣻ������������˵�����ɣ�
��2����S��ACP=8����ֱ��l2�ĺ�����ϵʽ��
��3������M��0��6����ƽ����x���ֱ��l3����QΪֱ��l3��һ�����㣬����QABΪ����������ʱ�������е�Q�����꣮
���𰸡���1��. ֱ��L2�����㣨��2��0������2��y=![]() x+1����3����Q������Ϊ��9��6����3��6����6��6����
x+1����3����Q��������9��6����3��6����6��6����![]() ��6����
��6����
����������1����y=kx+2k��
��y=k��x+2����
�൱x=��2ʱ��y=0��
��ֱ��L2�����㣨��2��0����
��2������y1=0�õ���![]() x+3=0�����x=6��
x+3=0�����x=6��
��A��6��0����
���ɣ�1����֪����C������Ϊ����2��0����
��AC=8��
��S��ACP=8��
��![]() =8����
=8����![]() =8��
=8��
��ã�Py=2��
�߽�y=2���멁![]() x+3=0�ã���
x+3=0���![]() x+3=2�����x=2��
x+3=2�����x=2��
���P��������2��2����
����P���������y=kx+2k�ã�2k+2k=2����ã�k=![]() ��
��
��ֱ��L2�Ľ���ʽΪ![]() ��
��
��3���߽�x=0����y=��![]() x+3�ã�y=3��
x+3�ã�y=3��
���B��������0��3����
���Q��������n��6����
�ٵ�QB=QAʱ���������ľ��빫ʽ�ã�n2+��6��3��2=��6��n��2+��6��0��2��
��ã�n=![]() ��
��
���Q��������![]() ��6����
��6����
�ڵ�BQ=BAʱ���������ľ��빫ʽ�ã�n2+��6��3��2=��6��0��2+��3��0��2��
��ã�n=6��n��6��
���Q��������6��6����6��6����
�߽�Q����6��6������y=��![]() �ã�y=��
�ã�y=��![]() ����6��+3=6��
����6��+3=6��
���Q��ֱ��AB�ϣ���ʱA��B��Q���ܹ��������Σ�
��Q����6��6������ȥ����
���Q��������6��6����
�۵�AB=AQʱ���������ľ��빫ʽ�ã���n��6��2+��6��0��2=��6��0��2+��3��0��2��
��ã�n=9��n=3��
���Q��������9��6����3��6����
������������Q��������9��6����3��6����6��6����![]() ��6����
��6����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ǻ���ֵ������ǣ���ȷ��1������
��1����֪sin��=0.5018�����������
��2����֪tan��=5�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ش�ʯˮ�⣬�ܿ�����Ϊ11960�������ף�11960���ÿ�ѧ��������ʾΪ�� ��
A.1.196��108
B.1.196��107
C.11.96��107
D.0.1196��109
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г������������¼��DZ�Ȼ�¼����ǣ�������
A.�������B.������C.��������D.ˮ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������εĶ���Ϊ80�㣬�����ĵǵĶ�����( )
A.20��
B.50��
C.60��
D.80��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.��a3��2=a6
B.aa2=a2
C.a3+a2=a6
D.��3a��3=9a3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��![]() -��+3.7��+��+
-��+3.7��+��+![]() ��-��-1.7�� ��2����-72����2
��-��-1.7�� ��2����-72����2![]() ����-
����-![]() ������-3
������-3![]() ��
��
��3����![]() -
-![]() -
-![]() +
+![]() ������-24�� ��4��-32����-2��+42����-2��3-�O-22�O
������-24�� ��4��-32����-2��+42����-2��3-�O-22�O
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε�һ���ڽ�Ϊ50�������Ķ��ǵĶ����ǣ� ��
A.40��B.50��C.50����40��D.50����80��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ� ��
A.3x+2x2=5x2
B.��ab��ab=��2ab
C.2a2b��a2b=1
D.7x+5x=12x2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com