
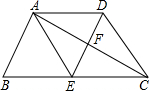
 如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
|


科目:初中数学 来源: 题型:
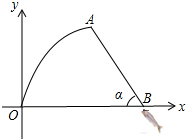 某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.
某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
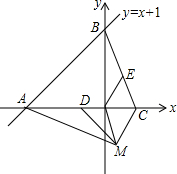 如图,在平面直角坐标系中直线y=x+1与坐标轴交于AB两点,AB=AC,D、E分别为AC、BC的中点,作∠CDM=45°,AM⊥CM,
如图,在平面直角坐标系中直线y=x+1与坐标轴交于AB两点,AB=AC,D、E分别为AC、BC的中点,作∠CDM=45°,AM⊥CM,查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
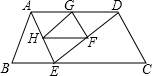 如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH.
如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com