

分析 (1)以直径为斜边,直角边分别为2和6的圆内接直角三角形满足要求;
(2)以直径为斜边,直角边分别为2$\sqrt{2}$和4$\sqrt{2}$的圆内接直角三角形满足要求;
(3)以直径为斜边,直角边为2$\sqrt{5}$的圆内接等腰直角三角形满足要求.
解答 解:(1)如图1所示,△ABC即为所求三角形,其中AC=2,BC=6;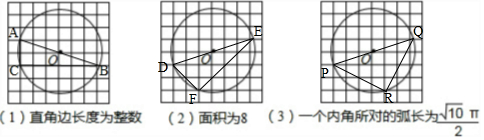
(2)如图2所示,△DEF即为所求作三角形,其中DF=2$\sqrt{2}$,EF=4$\sqrt{2}$,
则其面积为$\frac{1}{2}$×2$\sqrt{2}$×4$\sqrt{2}$=8;
(3)如图3所示,△PQR即为所求作三角形,其中PR=QR,∠PRQ=90°,
∵PQ=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∴∠PRQ所对弧长为$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$π.
点评 本题主要考查了圆周角定理的推论、勾股定理、弧长公式等知识点,理解新定义是解题的根本,熟练掌握直径所对圆周角是直角是解题的关键.


科目:初中数学 来源:2017届吉林省九年级下学期第二次月考数学试卷(解析版) 题型:填空题
如图,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,则EC的长为_________.

查看答案和解析>>
科目:初中数学 来源:2017届辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:判断题
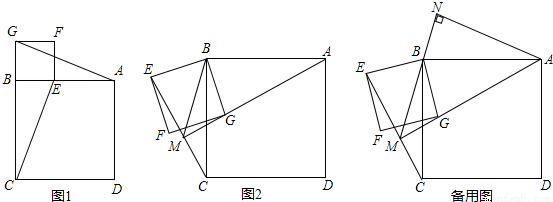
如图,四边形ABCD、BEFG均为正方形,
(1)如图1,连接AG、CE,试判断AG和CE的数量和位置关系并证明.
(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB的度数;若发生变化,请说明理由.
(3)在(2)的条件下,过点A作AN⊥MB交MB的延长线于点N,请直接写出线段CM与BN的数量关系.
查看答案和解析>>
科目:初中数学 来源:2017届辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:单选题
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=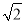 AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
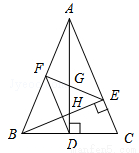
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
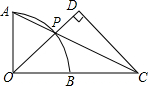 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com