
 如图,在四边形ABCD中,点E在CB的延长线上,对角线AC平分∠BCD,∠ABE=∠ABD,若∠BDC=80°,则∠ADB等于50°.
如图,在四边形ABCD中,点E在CB的延长线上,对角线AC平分∠BCD,∠ABE=∠ABD,若∠BDC=80°,则∠ADB等于50°. 分析 先过点A作AF⊥CE于F,作AG⊥BD于G,作AH⊥CD于H,根据角平分线的性质得出AH=AG,再根据AG⊥BD,AH⊥CD,得出点A在∠BDH的角平分线上,进而求得∠ADB的度数.
解答 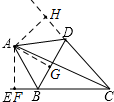 解:过点A作AF⊥CE于F,作AG⊥BD于G,作AH⊥CD于H,
解:过点A作AF⊥CE于F,作AG⊥BD于G,作AH⊥CD于H,
∵AC平分∠BCD,∠ABE=∠ABD,
∴AF=AH,AF=AG,
∴AH=AG,
∵AG⊥BD,AH⊥CD,
∴点A在∠BDH的角平分线上,
即∠ADB=$\frac{1}{2}$∠BDH=$\frac{1}{2}$(180°-∠BDC)=$\frac{1}{2}$(180°-80°)=50°.
故答案为:50°.
点评 本题主要考查了多边形的内角与外角,解决问题的关键是作辅助线,运用角平分线的性质定理及其判定定理进行推导计算.解题时注意:角内部到角两边距离相等的点在这个角的平分线上.


科目:初中数学 来源: 题型:选择题
 如图,已知直线l:y=2x,分别过x轴上的点A1(1,0)、A2(2,0)、…、An(n,0),作垂直于x轴的直线交l于点B1、B2、…、Bn,将△OA1B1,四边形A1A2B2B1、…、四边形An-1AnBnBn-1的面积依次记为S1、S2、…、Sn,则Sn=( )
如图,已知直线l:y=2x,分别过x轴上的点A1(1,0)、A2(2,0)、…、An(n,0),作垂直于x轴的直线交l于点B1、B2、…、Bn,将△OA1B1,四边形A1A2B2B1、…、四边形An-1AnBnBn-1的面积依次记为S1、S2、…、Sn,则Sn=( )| A. | n2 | B. | 2n+1 | C. | 2n | D. | 2n-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com