
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
【答案】
(1)解:设甲种商品应购进x件,乙种商品应购进y件.
根据题意得: ![]() .
.
解得: ![]() .
.
答:甲种商品购进100件,乙种商品购进80件
(2)解:设甲种商品购进a件,则乙种商品购进(180﹣a)件.
根据题意得 ![]() .
.
解不等式组,得60<a<64.
∵a为非负整数,∴a取61,62,63
∴180﹣a相应取119,118,117
方案一:甲种商品购进61件,乙种商品购进119件.
方案二:甲种商品购进62件,乙种商品购进118件.
方案三:甲种商品购进63件,乙种商品购进117件.
答:有三种购货方案,其中获利最大的是方案一
【解析】1)等量关系为:甲件数+乙件数=180;甲总利润+乙总利润=1240.(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量<5040;甲总利润+乙总利润>1312.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中( ).
A. 只有一个直角 B. 只有一个锐角 C. 有两个直角 D. 有两个钝角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为正方形,AB=2![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家体育馆“鸟巢”的建筑面积达25.8万平方米,请将“25.8万”用科学记数法表示,结果是( )
A.25.8×104
B.25.8×105
C.2.58×104
D.2.58×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校食堂的中餐与晚餐的资费标准如下:
种类 | 单价 |
米饭 | 0.5元/份 |
A类套餐菜 | 3.5元/份 |
B类套餐菜 | 2.5元/份 |
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?
查看答案和解析>>
科目:初中数学 来源: 题型:
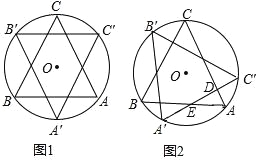
【题目】如图,边长为2的等边△ABC内接于⊙O,△ABC绕圆心O顺时针旋转得到△A′B′C′,A′C′分别交于点E、D,设旋转角为a(0°<a<360°).
(1)当a= 时,△A′′BC′与△ABC出现旋转过程中的第一次完全重合.
(2)当a=60°(如图1),该图
A,是中心对称图形但不是轴对称图形 B.是轴对称图形但不是中心对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形也不是中心对称图形
(3)如图2,当0°<a<120°时,△ADE的周长是否会发生变化?若会变化,请说明理由,若不会变化,求出它的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com