
 (2012•佛山)如图,直尺、三角尺都和圆O相切,AB=8cm.求圆O的直径.
(2012•佛山)如图,直尺、三角尺都和圆O相切,AB=8cm.求圆O的直径.| 1 |
| 2 |
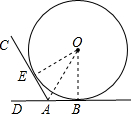 连接OE、OA、OB,
连接OE、OA、OB,| 1 |
| 2 |
| 1 |
| 2 |
| OA2-AB2 |
| 162-82 |
| 3 |
| 3 |
| 3 |
| 3 |


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
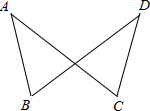 (2012•佛山)如图,已知AB=DC,DB=AC
(2012•佛山)如图,已知AB=DC,DB=AC查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•佛山)如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )
(2012•佛山)如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是( )查看答案和解析>>
科目:初中数学 来源: 题型:
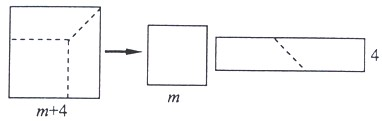 部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为
部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为查看答案和解析>>
科目:初中数学 来源: 题型:
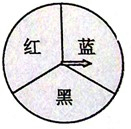 (2012•佛山)用如图所示的三等分的圆盘转两次做“配紫色(红色+蓝色)”游戏,配出紫色的概率用公式P=
(2012•佛山)用如图所示的三等分的圆盘转两次做“配紫色(红色+蓝色)”游戏,配出紫色的概率用公式P=| n | m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com