
| 2 |
| 7 |
| 5 |
| 7 |
| 1002 |
| (992+198+1)2 |
| 2 |
| 7 |
| 2 |
| 7 |
| 4 |
| 49 |
| 45 |
| 49 |
| 1002 |
| (99+1)2 |
| 1002 |
| 1002 |


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
 早7点整,芳芳以50米/分的速度步行去上学,妈妈同时骑自行车向相反方向去上班,10分钟时妈妈接到芳芳的电话,立即原速返回并前往学校,恰好与芳芳同时到达.她们离家的距离y(米)与行走时间x(分)间的函数关系如图,则她们到达学校的时间是( )
早7点整,芳芳以50米/分的速度步行去上学,妈妈同时骑自行车向相反方向去上班,10分钟时妈妈接到芳芳的电话,立即原速返回并前往学校,恰好与芳芳同时到达.她们离家的距离y(米)与行走时间x(分)间的函数关系如图,则她们到达学校的时间是( )| A、7点20分 |
| B、7点25分 |
| C、7点30分 |
| D、7点35分 |
查看答案和解析>>
科目:初中数学 来源: 题型:
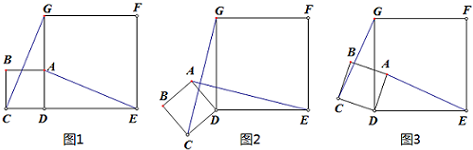
查看答案和解析>>
科目:初中数学 来源: 题型:
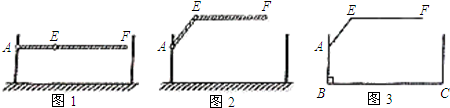
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,设D为BC上任意一点,点D不与B、C重合,且DC=x,若三角形ABD的面积为y.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,设D为BC上任意一点,点D不与B、C重合,且DC=x,若三角形ABD的面积为y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com