
 如图,点C是路段AB的中点,小明和小红两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,并且DA⊥AB于A,EB⊥AB于B.此时小明到路段AB的距离是50米,则小红到路段AB的距离是
如图,点C是路段AB的中点,小明和小红两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,并且DA⊥AB于A,EB⊥AB于B.此时小明到路段AB的距离是50米,则小红到路段AB的距离是 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
 小车安全是近几年社会关注的重大问题,超速和超载是主要的安全隐患,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:现在公路旁边选取一点A,再在笔直的车道1上确定点B,使AB与1垂直,测得AB的长为30米,在1上和点B的同侧选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.
小车安全是近几年社会关注的重大问题,超速和超载是主要的安全隐患,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:现在公路旁边选取一点A,再在笔直的车道1上确定点B,使AB与1垂直,测得AB的长为30米,在1上和点B的同侧选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
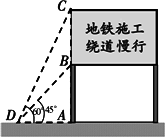
 显示牌(如图).已知立杆AB高度是3cm,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
显示牌(如图).已知立杆AB高度是3cm,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.查看答案和解析>>
科目:初中数学 来源:2010年湖南省长沙市初中毕业学业水平考试数学试卷 题型:044
为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3 m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点C是路段AB的中点,小明和小红两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,并且DA⊥AB于A,EB⊥AB于B.此时小明到路段AB的距离是50米,则小红到路段AB的距离是________米.
如图,点C是路段AB的中点,小明和小红两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,并且DA⊥AB于A,EB⊥AB于B.此时小明到路段AB的距离是50米,则小红到路段AB的距离是________米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com